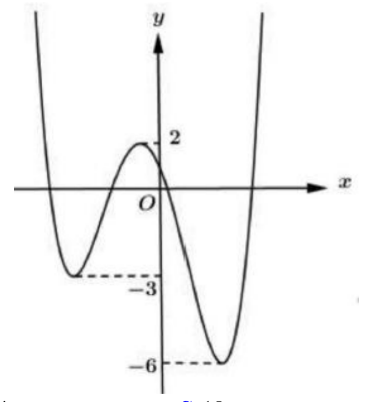
Cho y=f(x) là hàm đa thức bậc 4 và có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-12 ; 12] để hàm số \(g(x)=|2 f(x-1)+m \mid\) có 5 điểm cực tri?
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiĐặt \(t=x-1\) khi đó ta có \(y=g(t+1)=12 f(t)+m \mid=\sqrt{(2 f(t)+m)^{2}}\)
\(\begin{array}{l} \Rightarrow y^{\prime}=\frac{2(2 f(t)+m) \cdot 2 f^{\prime}(t)}{2 \sqrt{(2 f(t)+m)^{2}}}=\frac{2[2 f(t)+m] f^{\prime}(t)}{\sqrt{(2 f(t)+m)^{2}}} \\ y^{\prime}=0 \Leftrightarrow\left[\begin{array}{l} 2 f(t)+m=0 \\ f^{\prime}(t)=0 \end{array}\right. \end{array}\)
Đề hàm số \(y=g(t+1)=|2 f(t)+m|\) có 5 điểm cực trị thì phương trình \(y^{\prime}=0\) phai có 5 nghiệm bội lè phân biệt.
Dựa vào đồ thị hàm số ta thấy phương trình \(f^{\prime}(t)=0\) có 3 nghiệm đơn phân biệt \(\Rightarrow \) phương trình \(2 f(t)+m=0 \Leftrightarrow f(t)=-\frac{m}{2}\) phải có 2 nghiệm bội lẻ phân biệt.
\(\Rightarrow\) Đương thẳng \(y=-\frac{m}{2}\) cắt đồ thị hàm số y=f(t) tai 2 điểm phân biệt.
\(\Leftrightarrow\left[\begin{array}{l} -6<-\frac{m}{2} \leq-3 \\ -\frac{m}{2} \geq 2 \end{array} \Leftrightarrow\left[\begin{array}{l} 3 \leq \frac{m}{2}<6 \\ \frac{m}{2} \leq-2 \end{array} \Leftrightarrow\left[\begin{array}{l} 6 \leq m<12 \\ m \leq-4 \end{array}\right.\right.\right.\)
Kết hợp điều kiện \([-12 ; 12] \Rightarrow m \in[-12 ;-4] \cup[6 ; 12)\)
Mà \(n \in \mathbb{Z} \Rightarrow m \in\{-12 ;-11 ; \ldots ;-4 ; 6 ; 7 ; \ldots ; 11\}\)
Vậy có 15 giá trị m thỏa mãn yêu cầu bài toán.
Đề thi thử tốt nghiệp THPT QG môn Toán năm 2020
Trường THPT chuyên Thái Bình
Câu hỏi liên quan
-
Cho hinh chóp S . A B C D có \(S A \perp(A B C D)\), đáy ABCD là hình chữ nhật có \(A B=a \sqrt{3}, A D=a \sqrt{2}\) Khoảng cách giũra SD và BC bằng:
-
Biết \(\int\limits_{0}^{1} \frac{3 x-1}{x^{2}+6 x+9} d x=3 \ln \frac{a}{b}-\frac{5}{6},\) trong đó a, b là các số nguyên dương và \(\frac{a}{b}\) tối gian. Khi dó \(a^{2}-b^{2}\) bằng
-
Hình lăng trụ đứng \(A B C . A^{\prime} B^{\prime} C^{\prime}\) có đáy ABC là tam giác vuông cân tại A có bao nhiêu mặt phẳng đối xứng?
-
Cho a, b, c là các số thực dương khác 1. Hình vẽ bên là đồ thị của ba hàm số \(y=\log _{a} x, y=\log _{b} x, y=\log _{c} x .\)Mệnh đề nào dưới đây đúng?
-
Viết phương trình tiếp tuyến của đồ thị hàm số \(y=\frac{x+3}{x-1},\) biết tiếp tuyến đó tạo với hai trục tọa độ một tam giác vuông cân.
-
Trong không gian Oxyz, hai mặt phẳng \(x-4 y+2 z-7=0\,\, và \,\,2 x-2 y+z+4=0\) chứ hai mặt của hình lập phương. Thề tích khối lập phương đó là:
-
Trên giá sách có 4 quyển sách toán, 3 quyển sách lý, 2 quyển sách hóa (các quyển sách cùng đôi một khác nhau). Hỏi có bao nhiêu cách lấy ra 3 quyển sách sao cho ít nhất một quyển sách toán?
-
Tính \( \lim\limits _{x \rightarrow 0^{+}} \frac{x-\sqrt{x}}{x}\)
-
Hàm số \(y=\log _{\frac{\pi}{3}}(x-1)\) nghịch biến trên khoảng nào dưới đây?
-
Cho hàm số f(x) xác định và liên tục trên \(\mathbb{R} \backslash\{-1\},\) có bång biên thiên nhur sau:
Höi đồ thị hàm số \(y=\frac{1}{f(x)}\) có tất cả bao nhiêu đường tiệm cận đứng và tiệm cận ngang?
-
Tìm tất cả các giá trị của m đẻ phương trình \(2^{2 x-1}+m^{2}-m=0\) có nghiệm.
-
Cho \(\left(u_{n}\right)\) là cấp số nhân \(u_{1}=2, q=3\,. Tính\,\,u_{3}\)
-
Tính thề tích V của khối trụ có chu vi đáy là \(2 \pi,\) chiều cao là \(\sqrt{2}\)
-
Cho hàm số y=f(x) thòa mãn f(2)=16 và \(\int\limits_{0}^{2} f(x) d x=4 .\) Tinh \(\int\limits_{0}^{1} x \cdot f^{\prime}(2 x) d x\)
-
Trong không gian Oxyz, cho hai mặt phẳng \((\alpha): x+y-z+1=0\,\,và \,\,(\beta):-2 x+m y+2 z-2=0\) Tìm m để \((\alpha)\) song song với \((\beta)\)
-
Tập hợp các điềm biều diễn số phúrc z thỏa mãn \(|2 z-1|=1 \)là:
-
Tìm họ nguyên hàm của hàm số \(f(x)=\sin 3 x\)
-
Cho số thực x thỏa mãn \(2^{x^{2}} \cdot 3^{x+1}=1\). Mệnh đề nào dưới đây đúng?
-
Nếu \(\int\limits_{0}^{m}(2 x-1) d x=2\) thì m có giá trị bằng:
-
Cho hình lăng trụ \(A B C . A^{\prime} B^{\prime} C^{\prime}\) có đáy ABC là tam giác vuông tại A . Cạnh BC=2a và \(\widehat{ A B C}=60^{\circ}\) .Biết tứ giác \(B C C^{\prime} B^{\prime}\) là hinh thoi có \(\widehat{ B^{\prime} B C}\) nhon. Măt phăng \(\left(B C C^{\prime} B^{\prime}\right)\) vuông góc vói (A B C) và măt phẳng \(\left(A B B^{\prime} A^{\prime}\right)\) tạo với (A B C) góc \(45^{\circ} .\) Thể tích khối lăng trụ \(A B C . A^{\prime} B^{\prime} C^{\prime}\) bằng:
