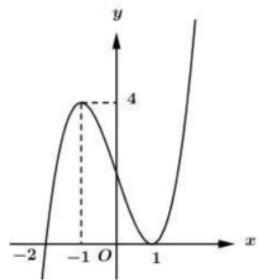
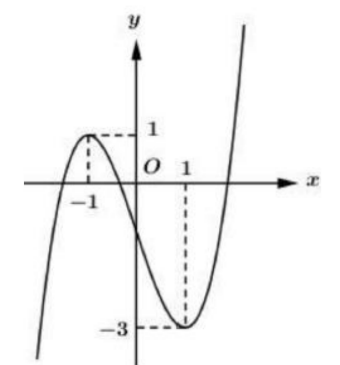
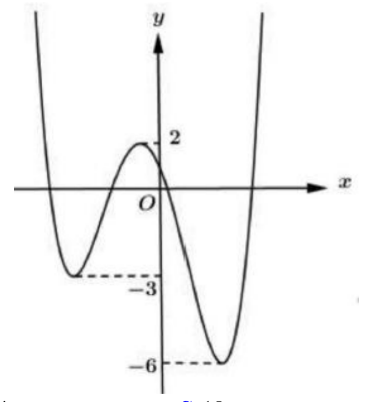
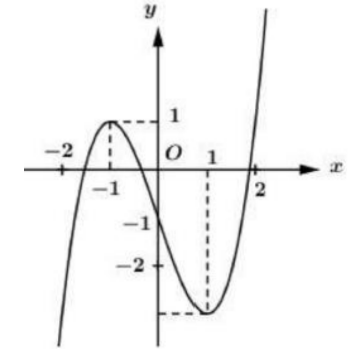
Cho y=f(x) là hàm đa thức bậc 3 và có đồ thị nhu hình vẽ bên. Hỏi phương trình \(f[f(\cos x)-1]=0\) có bao nhiêu nghiệm thuộc đoan \([0 ; 3 \pi] ?\)
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiĐặt \(t=f(\cos x)-1\) phương trình trở thành:\(f(t)=0\)
\(\text { Với } x \in[0 ; 3 \pi] \Rightarrow-1 \leq \cos x \leq 1 \Leftrightarrow-3 \leq f(\cos x) \leq 1 \Rightarrow-4 \leq f(\cos x)-1 \leq 0 \Rightarrow t \in[-4 ; 0]\)
Dựa vào đồ thị hàm số ta thấy \(f(t)=1 \Leftrightarrow\left[\begin{array}{l}t=t_{1} \in(-2 ;-1) \\ t=t_{2} \in(-1 ; 0) \\ t=t_{3} \in(1 ; 2)(k t m)\end{array}\right.\)
\(+ Với \,t=t_{1} \Rightarrow f(\cos x)-1=t_{1} \Leftrightarrow f(\cos x)=t_{1}+1 \in(-1 ; 0)\)
Dụa vào đồ thị hàm số ta có: \(f(\cos x)=t_{1}+1 \in(-1 ; 0) \Leftrightarrow\left[\begin{array}{l}\cos x=a_{1} \in(-2 ;-1)(\text { Vô nghiệm }) \\ \cos x=a_{2} \in(-1 ; 0)(1) \\ \cos x=a_{3} \in(1 ; 2)(\text { Vô nghiệm })\end{array}\right.\)
Trên đoạn \([0 ; 3 \pi]\) phương trình (1) có 3 nghiệm phân biệt.
\(+\text { Với } t=t_{2} \Rightarrow f(\cos x)-1=t_{2} \Leftrightarrow f(\cos x)=t_{2}+1 \in(0 ; 1)\)
Dụa vào đồ thị hàm số ta có: \(f(\cos x)=t_{2}+1 \in(0 ; 1) \Leftrightarrow\left[\begin{array}{l}{\left.\cos x=b_{1} \in(-2 ;-1)(\text { Vô nghiệm })\right.} \\ \cos x=b_{2} \in(0 ; 1)(2) \\ \cos x=b_{3} \in(1 ; 2)(\text { Vô nghiệm })\end{array}\right.\)
Trên đoạn \([0 ; 3 \pi]\) phương trình (2) có 3 nghiệm phân biệt.
Vậy phương trình đã cho có 6 nghiệm phân biệt.
Đề thi thử tốt nghiệp THPT QG môn Toán năm 2020
Trường THPT chuyên Thái Bình