Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau
Số nghiệm thuộc đoạn \(\left[ -\pi ;2\pi \right]\) của phương trình \(4f\left( \cos 2x \right)+5=0\) là
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiĐặt \(t=2x\xrightarrow{x\in \left[ -\pi ;2\pi \right]}t\in \left[ -2\pi ;4\pi \right]\).
Phương trình \(4f\left( \cos t \right)+5=0\Leftrightarrow f\left( \cos t \right)=-\frac{5}{4}\)
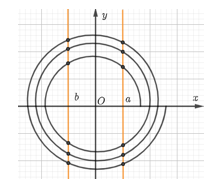
\(\left[ \begin{align} & \cos t=m<-1\,,\left( VN \right) \\ & \cos t=b\in \left( -1;0 \right),\,\left( 2 \right) \\ & \cos t=a\in \left( 0;1 \right),\,\,\,\,\,\left( 3 \right) \\ & \cos t=n>1,\,\,\left( VN \right) \\ \end{align} \right.\)
Từ đồ thị hàm số suy ra phương trình \(\left( 2 \right),\left( 3 \right)\) mỗi phương trình có đúng \(6\) nghiệm. Vậy phương trình đã cho có \(12\) nghiệm.
Đề thi thử tốt nghiệp THPT môn Toán năm 2023
Trường THPT Võ Thị Sáu
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)











