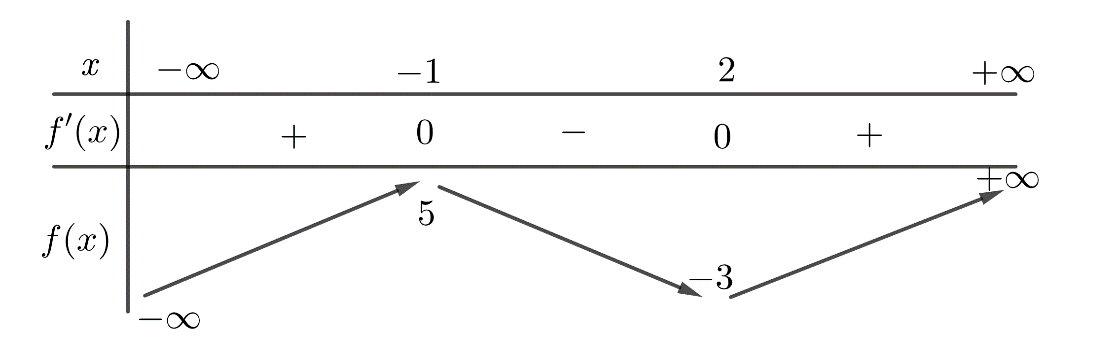Cho hàm số \(y=f\left( x \right)\), hàm số \(y={f}'\left( x \right)\) liên tục trên \(R\) và có đồ thị như hình vẽ.
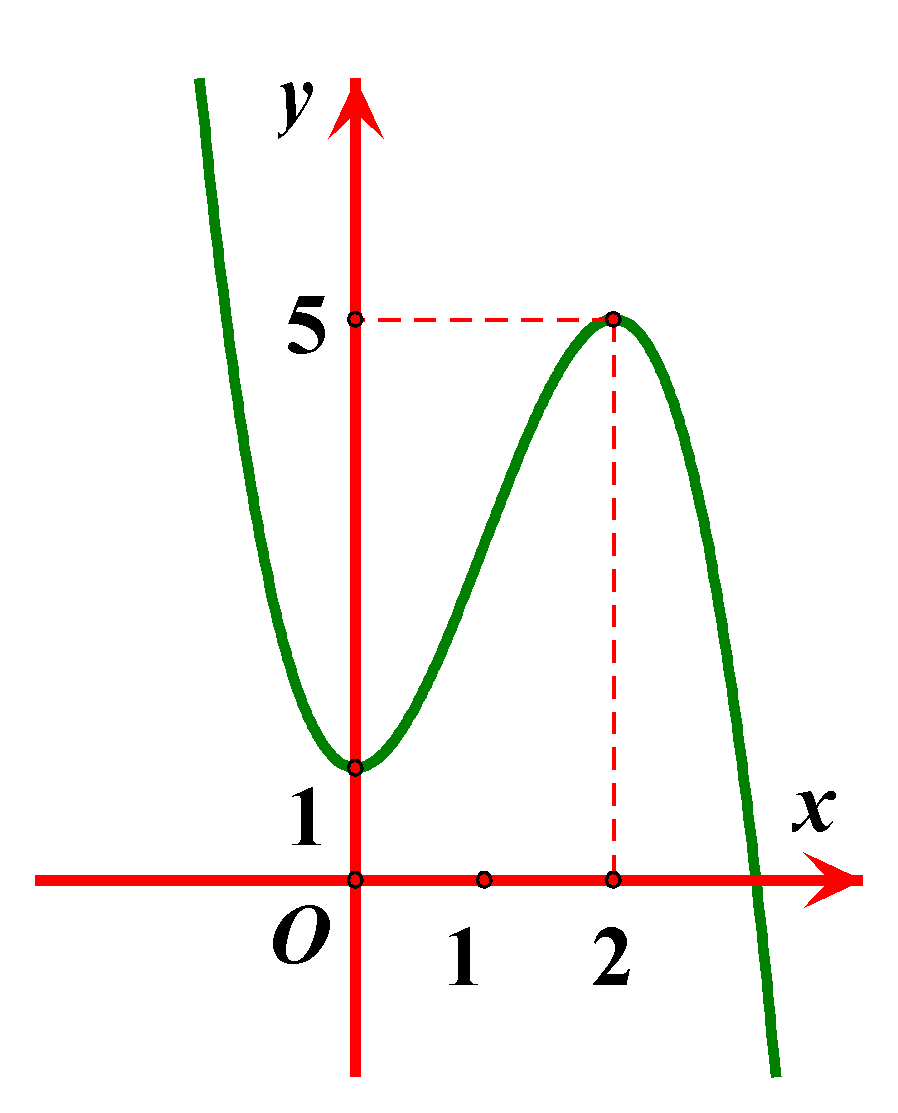
Bất phương trình \(f\left( x \right)-{{\left( x-1 \right)}^{3}}>m+5x+1\) (với \(m\) là tham số thực) nghiệm đúng với mọi \(x\in \left( 0\,;\,3 \right)\) khi và chỉ khi
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiT a có \(f\left( x \right)-{{\left( x-1 \right)}^{3}}>m+5x+1,\,\forall \,x\in \left( 0\,;\,3 \right)\)
\(\Leftrightarrow f\left( x \right)-\left( {{x}^{3}}-3{{x}^{2}}+8x \right)>m,\,\forall \,x\in \left( 0\,;\,3 \right)\) \(\Leftrightarrow m<\underset{\left( 0\,;\,3 \right)}{\mathop{\min }}\,\left[ f\left( x \right)-\left( {{x}^{3}}-3{{x}^{2}}+8x \right) \right],\,\forall \,x\in \left( 0\,;\,3 \right)\)
Đặt \(h\left( x \right)=f\left( x \right)-\left( {{x}^{3}}-3{{x}^{2}}+8x \right)\)
Có \({h}'\left( x \right)={f}'\left( x \right)-\left( 3{{x}^{2}}-6x+8 \right)={f}'\left( x \right)-\left[ 3{{\left( x-1 \right)}^{2}}+5 \right]\).
Từ đồ thị ta thấy trên khoảng \(\left( 0\,;\,3 \right)\) thì \({f}'\left( x \right)\le 5\). Mặt khác \(\left[ 3{{\left( x-1 \right)}^{2}}+5 \right]\ge 5\) nên \({h}'\left( x \right)\le 0,\,\forall \in \left( 0\,;\,3 \right)\).
Ta có hàm số \(y=h\left( x \right)\) nghịch biến trên khoảng \(\left( 0\,;\,3 \right)\) nên từ \(m<\underset{\left( 0\,;\,3 \right)}{\mathop{\min }}\,\left[ f\left( x \right)-\left( {{x}^{3}}-3{{x}^{2}}+8x \right) \right],\,\forall \,x\in \left( 0\,;\,3 \right)\Leftrightarrow m\le f\left( 3 \right)-24\).
Đề thi thử tốt nghiệp THPT môn Toán năm 2023
Trường THPT Nguyễn Kiệm
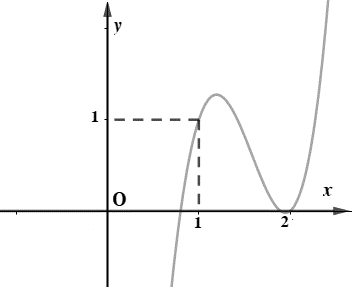
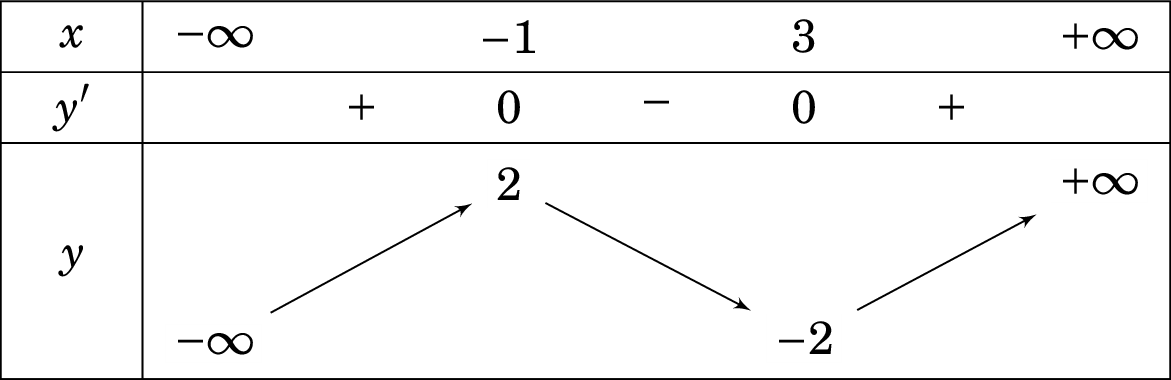
.png)