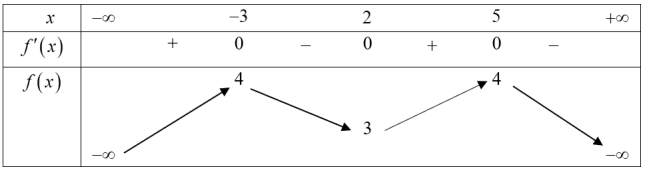
Cho hàm số y=f(x) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình vẽ:
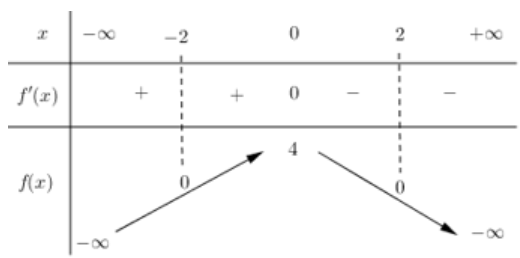
Có bao nhiêu giá trị nguyên của m để phương trình \(f( \sqrt{1+x}-\sqrt{3-x})=f( \sqrt{|m|+1})\) có nghiệm?
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiPhương trình \(f( \sqrt{1+x}-\sqrt{3-x})=f( \sqrt{|m|+1})\,\,\,\,(1)\).
ĐK: \(x\in [-1;3]\)
\(\text { Đặt } t=\sqrt{1+x}-\sqrt{3-x}\)
Xét hàm số \(g (x)=\sqrt{1+x}-\sqrt{3-x}, x\in [-1;3]\)
Ta có \(g^{\prime}( x)=\frac{1}{2 \sqrt{1+x}}+\frac{1}{2 \sqrt{3-x}}>0, \,\forall x \in(-1 ; 3)\Rightarrow g(x)\) đồng biến trên khoảng (-1;3).
do đó khi \(x\in [-1;3] \Rightarrow t \in[g(-1) ; g( 3)] \text { hay } t \in(-2 ; 2)\)
+ Phương trình (1) trở thành \(f (t)=f( \sqrt{|m|+1})\)(2)
Phương trình (1) có nghiệm \(\Leftrightarrow \) phương trình (2) có nghiệm \(t \in[-2 ; 2]\).
\(\Leftrightarrow\) đường thẳng\(y=f (\sqrt{|m|+1})\) cắt đồ thị hàm số y=f(t) tại ít nhất một điểm có hoành độ thuộc [-2;2].
+ ta có bảng biến thiên:
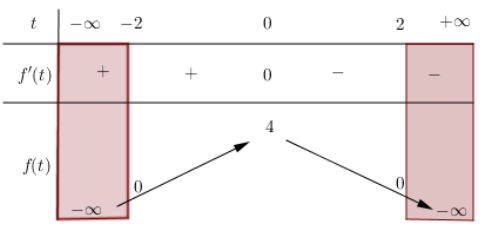
Suy ra phương trình (1) có nghiệm
\(\Leftrightarrow 0 \leq f(\sqrt{|m|+1}) \leq 4\)
\(\begin{array}{l} \Leftrightarrow-2 \leq \sqrt{|m|+1} \leq 2 \\ \Leftrightarrow|m|+1 \leq 4 \\ \Leftrightarrow-3 \leq m \leq 3 \end{array}\)
Vậy có 7 giá trị nguyên của m thỏa mãn yêu cầu bài toán.
Đề thi thử tốt nghiệp THPT QG môn Toán năm 2020
Trường THPT Nho Quan B