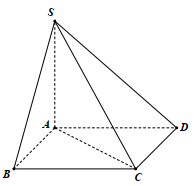
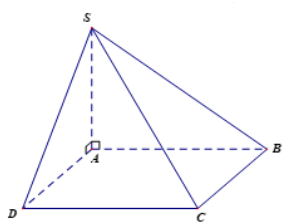
Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a , SA vuông góc với mặt phẳng (ABCD) và \(SC=a\sqrt3\) (minh họa như hình bên). Góc giữa mặt phẳng (SBC) và và mặt phẳng (ABCD) bằng

Câu hỏi liên quan

• Trong không gian, cho tam giác ABC vuông tại A, \(A B=a \text { và } A C=\sqrt{3} a\) . Tính độ dài đường sinh l của hình nón, nhận được khi quay tam giác ABC xung quanh trục AB .
   

• Có bao nhiêu cách chọn 2 học sinh từ nhóm có 5 học sinh.

• Tập xác định của hàm số: \(y=x^{\frac{2}{3}}\) là:

ZUNIA12

• Cho hai số thực dương x y ; thỏa mãn \(\log _{3} x+x y=\log _{3}(8-y)+x(8-x)\). Giá trị nhỏ nhất của biểu thức \(P=x^{3}-\left(x^{2}+y^{2}\right)-16 x\) bằng?

• Một người gửi tiết kiệm ngân hàng với lãi suất 0,5% mỗi tháng theo cách sau: mỗi tháng (vào đầu tháng) người đó gửi vào ngân hàng 10 triệu đồng và ngân hàng tính lãi suất (lãi suất không đổi) dựa trên số tiền tiết kiệm thực tế của tháng đó. Hỏi sau 5 năm, số tiền của người đó có được gần nhất với số tiền nào dưới đây (cả gốc và lãi, đơn vị triệu đồng)?

• Cho hàm số f (x)  liên tục trên \(\mathbb{R}\) và có bảng xét dấu của f '(x) như sau. Điểm cực đại của hàm số trên là

  

• Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, \(S A \perp(A B C D) \text { và } S A=a \sqrt{3}\)  . Khi đó thể tích của hình chóp S.ABCD  bằng:

  

• Tìm họ nguyên hàm của hàm số \(f(x)=e^{2020 x}\).

• Cho hình trụ T . Biết rằng khi cắt hình trụ T bới mặt phẳng (P) vuông góc với trục được thiết diện là đường tròn có chu vi \(6a\pi\) và cắt hình trụ T bởi mặt phẳng Q song song với trục và cách trục một khoảng bằng 2a, thiết diện thu được là một hình vuông. Tính thể tích khối trụ T.

• Trong không gian Oxyz , mặt phẳng \((P): x+2 y-3 z+1=0\) song song với mặt phẳng nào dưới đây ?

• Cho hàm số bậc ba y=f(x) có đồ thị trong hình bên. Số nghiệm của phương trình \(2 f(x)-3=0\) là:

  

• Trong không gian Oxyz , Cho mặt cầu \((S): x^{2}+y^{2}+z^{2}+2 x+2 y-4 z-3=0\). Đường kính của (S) là:

• Số giao điểm của đồ thị hàm số \(y=-x^{3}+3 x^{2}-7\) và trục hoành là:

• Cho hàm số y=f(x)  liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình vẽ:

  

  Có bao nhiêu giá trị nguyên của m để phương trình \(f( \sqrt{1+x}-\sqrt{3-x})=f( \sqrt{|m|+1})\) có nghiệm?

• Cho hàm số f(x) có bảng biến thiên như sau:

  

  Hàm số đã cho đồng biến trên khoảng nào dưới đây?

• Trong không gian Oxyz , hình chiếu vuông góc của A(2;1;1) lên mặt phẳng (Oyz) có tọa độ là:

• Thể tích của một khối lập phương cạnh \(1\over2\) bằng

• Trong buổi lễ phát thưởng cho các học sinh tiêu biểu, lớp 12A có 1 học sinh, lớp 12B có 4 học sinh, lớp 12C có 5 học sinh. Các học sinh được xếp thành một hàng ngang sao cho học sinh lớp 12A luôn đứng giữa một học sinh lớp 12B và một học sinh lớp 12C . Có bao nhiêu cách xếp như vậy?

• Trong không gian Oxyz , Cho đường thẳng \(\Delta:\left\{\begin{array}{l} x=2+t \\ y=-1-t \\ z=1 \end{array}\right.\).  Véc tơ nào dưới đây là một véc tơ chỉ phương của \(\Delta\)?

• Có bao nhiêu giá trị nguyên âm của tham số m để hàm số \(y=\frac{1}{4} x^{4}+m x-\frac{3}{2 x}\) đồng biến trên khoảng \((0;+\infty)\).