Cho hình lập phương ABCD. A' B' C' D' cạnh bằng 3a ,\(K \in C C^{\prime} \text { sao cho } C K=\frac{2}{3} C C^{\prime}\). Mặt phẳng \((\alpha)\) qua A,K và song song với \(B'D'\) chia khối lập phương trình hai phần. Tính thể tích phần khối đa diện chứa đỉnh C.
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai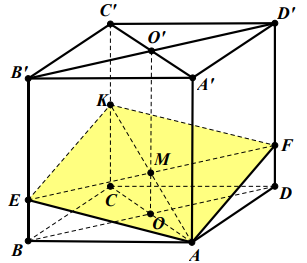
Gọi O, O' lần lượt là tâm của hình vuông ABCD, A 'B 'C' D'. \(M=A K \cap \mathrm{OO}^{\prime}\)
Qua M kẻ đường thẳng song song với BD cắt BB', DD' lần lượt tại E, F
Khi đó, thiết diện tạo bởi \((\alpha)\) và hình lập phương chính là hình bình hành AEKF.
Có OM là đường trung bình tam giác ACK nên \(\mathrm{OM}=\frac{1}{2} \mathrm{CK}=\frac{1}{2} \cdot \frac{2}{3} \mathrm{CC}^{\prime}=a\)
\(\text { Do dó, } B E=D F=\frac{1}{2} C K=\frac{a}{2}\)
Dễ thấy tứ giác \(B C K F=C^{\prime} B^{\prime} E K\)
mặt phẳng ( AA'C'C ) chia khối ABEKFDC thành hai phần bằng nhau nên:
\(V_{A B E K F D C}=2 V_{A. B C K E}=2 .\frac{1}{3} . A B. S_{B C K E}=\frac{2}{3}.3 a .\frac{1}{2} .S_{B C C' B'}=9 a^{3}\)
Đề thi thử tốt nghiệp THPT QG môn Toán năm 2020
Trường THPT Nho Quan B