Có bao nhiêu giá trị nguyên của tham số \(m\) để tập nghiệm của bất phương trình
\({{2023}^{\ln \left( 2{{x}^{2}}+4x+m \right)}}-{{2023}^{2\ln \left( 2x-1 \right)}}>0\) chứa đúng bốn số nguyên?
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiChọn B
Điều kiện:
\(\left\{ \begin{align} & 2x-1>0 \\ & 2{{x}^{2}}+4x+m>0 \\ \end{align} \right.\) \(\Leftrightarrow \left\{ \begin{align} & x>\frac{1}{2} \\ & 2{{x}^{2}}+4x+m>0 \\ \end{align} \right.\)
Ta có: \({{2023}^{\ln \left( 2{{x}^{2}}+4x+m \right)}}-{{2023}^{2\ln \left( 2x-1 \right)}}>0\Leftrightarrow \ln \left( 2{{x}^{2}}+4x+m \right)>2\ln \left( 2x-1 \right)\)
\(\Leftrightarrow 2{{x}^{2}}+4x+m>{{\left( 2x-1 \right)}^{2}}\)
\(\Leftrightarrow 2{{x}^{2}}-8x+1-m<0\)
\(\Leftrightarrow m>2{{x}^{2}}-8x+1\)
Xét \(f\left( x \right)=2{{x}^{2}}-8x+1\) với \(x>\frac{1}{2}\). Ta có đồ thị hàm số như sau:
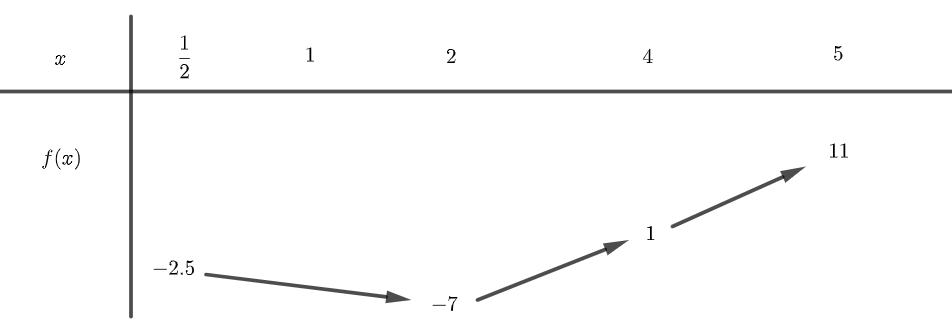
Để bất phương trình có đúng \(4\) nghiệm thì: \(1 < m \le 11\)
Vậy có \(10\) giá trị nguyên \(m\) thỏa mãn.
Đề thi thử tốt nghiệp THPT môn Toán năm 2023
Trường THPT Gia Định
.png)











