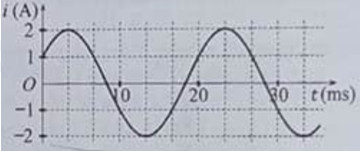
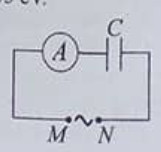
Đặt điện áp xoay chiều có giá trị hiệu dụng 120 V và tần số không đổi vào hai đầu đoạn mạch AB gồm điện trở R, cuộn dây có độ tự cảm L và điện trở r, tụ điện có điện dung C thay đổi được như hình bên. Khi C = Co hoặc C= 3Co thì độ lớn độ lệch pha giữa điện áp hai đầu đoạn mạch AB và điện áp hai đầu đoạn mạch MB là lớn nhất và bằng \(\Delta \varphi \) với \(\tan \Delta \varphi = 0,75\). Khi C = 1,5Co thì điện áp hiệu dụng giữa hai đầu R có giá trị gần nhất với giá trị nào sau đây?
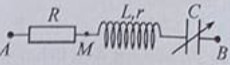
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai+ độ lệch pha giữa \({u_{MB}}\) và \({u_{AB}}\): \(\Delta \varphi \, = \,{\varphi _{MB}} - {\varphi _{AB}}\) và \(\tan \Delta \varphi \, = \,\frac{{\tan {\varphi _{MB}} - \tan {\varphi _{AB}}}}{{1 + \tan {\varphi _{MB}}.\tan {\varphi _{AB}}}}\)
\(\tan \Delta \varphi = \frac{{\frac{{\left( {{Z_L} - {Z_C}} \right)}}{r} - \frac{{\left( {{Z_L} - {Z_C}} \right)}}{{R + r}}}}{{1 + \frac{{\left( {{Z_L} - {Z_C}} \right)}}{r}.\frac{{\left( {{Z_L} - {Z_C}} \right)}}{{R + r}}}}\) = \(\frac{{\frac{{\left( {{Z_L} - {Z_C}} \right).R}}{{\left( {R + r} \right).r}}}}{{1 + \frac{{{{\left( {{Z_L} - {Z_C}} \right)}^2}}}{{\left( {R + r} \right).r}}}}\) = \(\frac{R}{{\frac{{\left( {R + r} \right)r}}{{\left( {{Z_L} - {Z_C}} \right)}} + \left( {{Z_L} - {Z_C}} \right)}}\)
Suy ra: (tanΔφ)max khi \(\left( {{Z_L} - {Z_C}} \right) = \pm \sqrt {\left( {R + r} \right)r} \) ( 1)
và \({\left( {\tan \Delta \varphi } \right)_{\max }} = \frac{R}{{2\sqrt {\left( {R + r} \right)r} }} = \frac{3}{4}\) ⇒ \(\frac{R}{r} = 3\)
Chuẩn hóa: r = 1 thì R =3 và từ (1) , ta được \({Z_L} - {Z_C} = \pm 2\) và \(\left\{ {\begin{array}{*{20}{c}}
{{Z_L} - {Z_{{C_o}}} = - 2}\\
{{Z_L} - \frac{{{Z_{{C_o}}}}}{3} = \,\,\,\,2}
\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{c}}
{{Z_{{C_o}}} = 6}\\
{{Z_L} = 4}
\end{array}} \right.\)
+ Khi C = 1,5CO ⇔ \({Z_C} = \frac{{{Z_{{C_o}}}}}{{1,5}} = 4\) = ZL ( cộng hưởng) . Lúc đó : \({U_R} = \frac{{R.U}}{{R + r}} = \frac{{3.120}}{4} = 90\,V\)
Đáp án D
Câu hỏi liên quan
-
Theo phương pháp giản đồ Fre-nen, một dao động điều hòa có phương trình \(x{\rm{ }} = {\rm{ }}4cos8\pi t\) (cm) (t tính bằng s) được biểu diễn bằng vectơ quay \(\overrightarrow {OM}\). Tốc độ góc của \(\overrightarrow {OM}\) là
-
Chiếu một chùm tia tử ngoại vào một tấm đồng thì các electron trên bề mặt tấm đông bật ra. Đây là hiện tượng
-
Trong thí nghiệm về giao thoa sóng ở mặt chất lỏng, hai nguồn kết hợp đặt tại A và B cách nhau 13 cm, dao động cùng pha cùng tần số 20 Hz theo phương thẳng đứng, phát ra hai sóng lan truyền trên mặt chất lỏng với tốc độ 50 cm/s. Ở mặt chất lỏng, M và N là hai điểm sao cho ABMN là hình thang cân có đáy MN dài 8 cm và đường cao dài 8 cm. Sổ điểm cực đại giao thoa trên đoạn thẳng MN là:
-
Đặt một điện áp xoay chiều vào hai đầu đoạn mạch gồm tụ điện có điện dung \(C = \frac{1}{{5\pi }}\) mắc nối tiếp với điện trở \(R = 50\Omega \). Hình bên là đồ thị biểu diễn sự phụ thuộc của cường độ dòng điện trong đoạn mạch theo thời gian t. Biểu thức điện áp giữa hai đầu đoạn mạch theo thời gian t (t tính bằng s) là:
-
Số nuclôn có trong hạt nhân \({}_3^7Li\) là
-
Chiều một chùm ánh sáng trắng, hợp tới mặt bên của một lăng kính. Sau khi qua lăng kính, chùm sáng bị phân tách thành các chùm sáng có màu khác nhau. Đây là hiện tượng
-
Hạt nhân \({}_6^{14}C\) có độ hụt khối bằng 0,1131 u. Biết \(1{\rm{ }}u{\rm{ }} = {\rm{ }}931,5{\rm{ }}MeV/{c^2}\). Năng lượng liên kết của hạt nhân \({}_6^{14}C\) là:
-
Tia nào sau đây có cùng bản chất với tia hồng ngoại?
-
Một điện tích điểm q dương được đặt trong điện trường đều có cường độ điện trường E. Độ lớn lực điện F tác dụng lên điện tích được tính bằng công thức nào sau đây?
-
Một dòng điện không đổi có cường độ I chạy qua điện trở R. Trong khoảng thời gian t, nhiệt lượng Q tỏa ra trên R được tính bằng công thức nào sau đây?
-
Trong thí nghiệm Y-âng về giao thoa ánh sáng, chiếu sáng hai khe đồng thời bằng hai bức xạ đơn sắc có bước sóng 720 nm và \(\lambda \left( {380nm < \lambda < 760nm} \right)\). Trên màn quan sát, O là vị trí của vân sáng trung tâm. Nếu \({\lambda} = {\lambda _1}\) thì điểm M trên màn là vị trí trùng nhau gần O nhất của hai vân sáng, trong khoảng OM (không kể O và M) có 5 vân sáng của bức xạ có bước sóng 720 nm. Nếu \(\lambda = {\lambda _2}\left( {{\lambda _2} \ne {\lambda _1}} \right)\) thì M vẫn là vị trí trùng nhau gần O nhất của hai vân sáng. Nếu chiếu sáng hai khe đồng thời chỉ bằng hai bức xạ có bước sóng \({\lambda _1}\) và \({\lambda _2}\) thì trong khoảng OM (không kể O và M) có tổng số vân sáng là:
-
Đặt một điện áp xoay chiều vào hai đầu một đoạn mạch có R, L, C mắc nối tiếp thì cảm kháng và dung kháng của đoạn mạch lần lượt là ZL và ZC. Nếu ZL = ZC thì độ lệch pha \(\varphi \) giữa điện áp hai đầu đoạn mạch và cường độ dòng điện trong đoạn mạch có giá trị nào sau đây?
-
Một nhạc cụ phát ra âm cơ bản hay họa âm thứ nhất có tần số \({f_o} = 440Hz\), nhạc cụ đó cũng đồng thời phát ra một loạt âm có tần số \(2{f_o};3{f_o}:4{f_o}\), gọi là các họa âm thứ hai, thứ ba, thứ tư,... Nhạc cụ này có thể phát ra họa âm có tần số nào sau đây?
-
Đặt một điện áp xoay chiều có giá trị hiệu dụng không đổi, tần số f thay đổi được vào hai đầu đoạn mạch MN gồm tụ điện C mắc nối tiếp với ampe kế A (ampe kế nhiệt) như hình bên. Khi tăng tần số f thì số chỉ của ampe kế thay đổi như thế nào?
-
Sóng truyền trên một sợi dây có hai đầu cố định với bước sóng \(\lambda \). Muốn có sóng dùng trên dây thì chiều dài l của dây thỏa mãn công thức nào sau đây?
-
Một con lắc lò xo gồm vật nhỏ khối lượng m và lò xo nhẹ có độ cứng k đang dao động điều hòa. Đại lượng \(T = 2\pi \sqrt {\frac{m}{k}}\), được gọi là:
-
Đặt điện áp xoay chiều có giá trị hiệu dụng 120 V và tần số không đổi vào hai đầu đoạn mạch mắc nối tiếp gồm điện trở, cuộn cảm thuần và tụ điện có điện dung C thay đổi được. Khi C = C0, hoặc \(C = \frac{{{C_0}}}{3}\) thì điện áp hiệu dụng giữa hai đầu điện trở có giá trị bằng nhau và bằng \(60\sqrt 3 V\). Khi \(C = \frac{{{C_0}}}{5}\) thì điện áp hiệu dụng giữa hai đầu cuộn cảm là:
-
Một mạch dao động LC lí tưởng gồm cuộn cảm thuần có độ tự cảm 2 mH và tụ điện có điện dung \(5\mu F\). Trong mạch đang có dao động điện tử tự do với cường độ dòng điện cực đại là 10 mA. Mốc thời gian là lúc cường độ dòng điện trong mạch có giá trị 10 mA. Tại thời điểm \(t = \frac{\pi }{{40}}\) ms thì điện tích của tụ điện là
-
Các nuclôn trong hạt nhân hút nhau bằng các lực rất mạnh tạo nên hạt nhân bền vững. Các lực hút đó gọi là là:
-
Lỗ trống là hạt tải điện trong môi trường nào sau đây?
