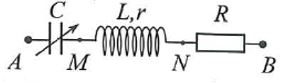
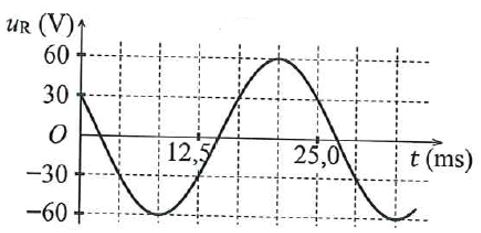
Đặt điện áp xoay chiều có giá trị hiệu dụng U và tần số không đổi vào hai đầu đoạn mạch gồm biến trở R, cuộn cảm thuần L và tụ điện C mắc nối tiếp. Khi \(R = {R_1}\) thì điện áp hiệu dụng giữa hai đầu L và hai đầu C lần lượt là \({U_{\rm{L}}}\) và \({U_{\rm{C}}}\) với \({U_{\rm{C}}} = 2{U_{\rm{L}}} = U\). Khi \(R = {R_2} = \frac{{{R_1}}}{{\sqrt 3 }}\) thì điện áp hiệu dụng giữa hai đầu L là 100V. Giá trị của U là:
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiChọn D.
Để đơn giản, ta chọn R1 = 1.
Khi R = R1, theo giả thuyết bài toán
\(\left\{ {\begin{array}{*{20}{c}} {{U_C} = 2{U_L}}\\ {{U_C} = U} \end{array} \Rightarrow \left\{ {\begin{array}{*{20}{c}} {{Z_C} = 2{Z_L}}\\ {{Z_C} = Z = \sqrt {R_1^2 + {{\left( {{Z_L} - {Z_C}} \right)}^2}} } \end{array}} \right.\;} \right.\)
\({\left( {2{Z_L}} \right)^2} = {\left( 1 \right)^2} + {\left( {{Z_L} - 2{Z_L}} \right)^2}\)
\(\Rightarrow \left\{ {\begin{array}{*{20}{c}} {{Z_L} = \frac{1}{{\sqrt 3 }}}\\ {{Z_C} = \frac{2}{{\sqrt 3 }}} \end{array}} \right.\;\left( 1 \right)\)
Khi \(R = \frac{{{R_1}}}{{\sqrt 3 }} = \frac{1}{{\sqrt 3 }}\), theo giả thuyết bài toán
\({U_L} = 100\;V\)
\(\frac{{U{Z_L}}}{{\sqrt {R_2^2 + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} = 100\;V\)
\(\mathop \Rightarrow \limits^{\left( 1 \right)} \frac{{U\left( {\frac{1}{{\sqrt 3 }}} \right)}}{{\sqrt {{{\left( {\frac{1}{{\sqrt 3 }}} \right)}^2} + {{\left( {\frac{1}{{\sqrt 3 }} - \frac{2}{{\sqrt 3 }}} \right)}^2}} }} = 100\;V\)
\(\Rightarrow U = 100\sqrt 2 \;V\)
Câu hỏi liên quan
-
Âm có tần số nằm trong khoảng từ 16Hz đến 20000Hz được gọi là:
-
Đặt điện áp \(u = 120\cos \left( {100\pi t - \frac{\pi }{6}} \right)\,\,(V)\) vào hai đầu đoạn mạch AB mắc nối tiếp gồm: tụ điện có điện dung C thay đổi được; cuộn dây có độ tự cảm L và điện trở r; điện trở R với R=2r như hình bên.
Khi C=C0 thì điện áp hiệu dụng giữa hai đầu đoạn mạch AN đạt cực tiểu. Khi \(C = \frac{{{C_0}}}{4}\) thì điện áp hiệu dụng giữa hai đầu đoạn mạch AM đạt cực đại và điện áp giữa hai đầu đoạn mạch MN là \({u_{{\rm{MN}}}}\). Biểu thức \({u_{{\rm{MN}}}}\) là:
-
Đặt điện áp xoay chiều có giá trị hiệu dụng U vào hai đầu một đoạn mạch chỉ có cuộn cảm thuần thì cảm kháng của đoạn mạch là ZL. Cường độ dòng điện hiệu dụng I trong đoạn mạch được tính bằng công thức nào sau đây?
-
Một sợi dây mềm có hai đầu cố định. Trên dây đang có sóng dừng và chỉ có một bụng sóng. Sóng truyền trên dây có bước sóng 120cm. Chiều dài của sợi dây là:
-
Trong thí nghiệm Y-âng về giao thoa ánh sáng, hai khe cách nhau 0,5mm, màn quan sát cách mặt phẳng chứa hai khe một khoảng D có thể thay đổi được. Chiếu sáng hai khe bằng ánh sáng đơn sắc có bước sóng \(\lambda \left( {380{\rm{\;nm}} \le \lambda \le 640{\rm{\;nm}}} \right)\). M và N là hai điểm trên màn cách vị trí vân sáng trung tâm lần lượt là 6,4mm và 9,6mmm. Ban đầu, khi \(D = {D_1} = 0,8{\rm{\;m}}\) thì tại M và N là vị trí của các vân sáng. Khi \(D = {D_2} = 1,6{\rm{\;m}}\) thì một trong hai vị trí của M và N là vị trí của vân tối. Tịnh tiến màn từ từ dọc theo phương vuông góc với mặt phẳng chứa hai khe và ra xa hai khe từ vị trí cách hai khe một đoạn D1 đến vị trí cách hai khe một đoạn D2. Trong quá trình dịch chuyển màn, số lần tại N là vị trí của vân sáng (không tính thời điểm ban đầu) là:
-
Đặt điện áp xoay chiều có giá trị hiệu dụng U vào hai đầu đoạn mạch có R, L, C mắc nối tiếp thì cường độ dòng điện hiệu dụng trong đoạn mạch là I. Gọi \(\cos \varphi \) là hệ số công suất của đoạn mạch. Công suất tiêu thụ điện của đoạn mạch là:
-
Trong thí nghiệm Y-âng về giao thoa ánh sáng đơn sắc, khoảng vân đo được trên màn quan sát là 0,08mm. Trên màn, khoảng cách giữa ba vân sáng liên tiếp là:
-
Một vật dẫn đang có dòng điện một chiều chạy qua. Trong khoảng thời gian \({\rm{\Delta }}t\), điện lượng dịch chuyển qua tiết diện thẳng của vật dẫn là \({\rm{\Delta }}q\). Cường độ dòng điện I trong vật dẫn được tính bằng công thức nào sau đây?
-
Ở một nơi trên mặt đất, hai con lắc đơn có chiều dài l và l+45 (cm) cùng được kích thích để dao động điều hòa. Chọn thời điểm ban đầu là lúc dây treo của hai con lắc đều có phương thẳng đứng. Khi độ lớn góc lệ̣ch dây treo của một con lắc so với phương thẳng đứng là lớn nhất lần thứ ba thì con lắc còn lại ở vị trí có dây treo trùng với phương thẳng đứng lần thứ hai (không tính thời điểm ban đầu). Giá trị của l là:
-
Tia X có cùng bản chất với tia nào sau đây?
-
Một vật dao động điều hòa dọc theo trục Ox với phương trình \(x = A{\rm{cos}}\left( {\omega t + \varphi } \right)\). Khi vật đi qua vị trí cân bằng thì độ lớn gia tốc của vật có giá trị là:
-
Một chất phóng xạ có hằng số phóng xạ là \(\lambda \). Chu kì bán rã T của chất phóng xạ này được tính bằng công thức nào sau đây?
-
Cấu tạo của máy phát điện xoay chiều một pha gồm hai bộ phận chính là:
-
Số nuclôn có trong hạt nhân \(\;_{40}^{90}{\rm{Zr}}\) là:
-
Pôlôni \(\;_{84}^{210}{\rm{Po}}\) là chất phóng xạ \(\alpha \) có chu kì bán rã 138 ngày và biến đổi thành hạt nhân chì \(\;_{82}^{206}{\rm{\;Pb}}\). Ban đầu (t=0), một mẫu có khối lượng 105,00 g trong đó 40% khối lượng của mẫu là chất phóng xạ pôlôni \(\;_{84}^{210}{\rm{Po}}\), phần còn lại không có tính phóng xạ. Giả sử toàn bộ các hạt \(\alpha \) sinh ra trong quá trình phóng xạ đều thoát ra khỏi mẫu. Lấy khối lượng của các hạt nhân bằng số khối của chúng tính theo đơn vị u. Tại thời điểm t=552 ngày, khối lượng của mẩu là:
-
Một khung dây dẫn phẳng, kín được đặt trong từ trường đều. Trong khoảng thời gian 0,05s, từ thông qua khung dây tăng đều từ 0 đến 0,02W. Trong khoảng thời gian trên, độ lớn của suất điện động cảm ứng xuất.
-
Ở một nơi trên mặt đất, con lắc đơn có chiều dài l dao động điều hòa với chu kì T. Cũng tại nơi đó, con lắc đơn có chiều dài \(\frac{l}{4}\) dao động điều hòa với chu kì là:
-
Một con lắc lò xo đang dao động điều hòa theo phương nằm ngang. Mốc thế năng ở vị trí cân bằng. Khi nói về cơ năng của con lắc, phát biểu nào sau đây sai?
-
Một sóng cơ có chu kỳ T, lan truyền trong một môi truờng với tốc độ v. Bước sóng \(\lambda \) được xác định bằng công thức nào sau đây?
-
Đặt điện áp xoay chiều u vào hai đầu đoạn mạch mắc nối tiếp gồm điện trở \(R = 40{\rm{\Omega }}\) và cuộn cảm thuần có độ tự cảm \(L = \frac{1}{{2\pi }}{\rm{H}}\). Hình bên là đồ thị biểu diễn sự phụ thuộc của điện áp \({u_{\rm{R}}}\) giữa hai đầu điện trở theo thời gian t. Biểu thức của u theo thời gian t (t tính bằng s) là:
