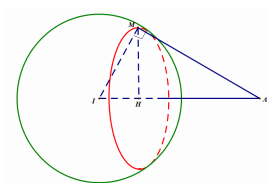
Trong không gian Oxyz, cho mặt cầu \(\left( S \right):{\left( {x + 1} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z + 1} \right)^2} = 9\) và điểm \(A\left( {2;3; - 1} \right)\). Xét các điểm M thuộc (S) sao cho đường thẳng AM tiếp xúc với (S), M luôn thuộc mặt phẳng có phương trình là 

Câu hỏi liên quan

• Có bao nhiêu số phức \(z\) thỏa mãn \(\left| z \right|\left( {z - 4 - i} \right) + 2i = \left( {5 - i} \right)z\)? 

• Trong không gian \(Oxyz\), mặt phẳng \(\left( P \right):x + 2y + 3z - 5 = 0\) có một vectơ pháp tuyến là:

• Cho hình lập phương \(ABCD.A'B'C'D'\) có tâm \(O\). Gọi \(I\) là tâm của hình vuông \(A'B'C'D'\) và \(M\) là điểm thuộc đoạn thẳng \(OI\) sao cho \(MO = 2MI\) (tham khảo hình vẽ). Khi đó côsin của góc tạo bởi hai mặt phẳng \(\left( {MC'D'} \right)\) và \(\left( {MAB} \right)\) bằng: 

  

ZUNIA12

• Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?

  

• Cho hàm số \(y = a{x^3} + b{x^2} + cx + d(a,b,c,d \in \mathbb{R})\) có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số đã cho là: 

  

• Có bao nhiêu giá trị nguyên của tham số \(m\) để hàm số \(y = {x^8} + \left( {m - 2} \right){x^5} - \left( {{m^2} - 4} \right){x^4} + 1\) đạt cực tiểu tại \(x = 0\)? 

• Trong không gian Oxyz, cho mặt cầu (S) có tâm \(I\left( { - 2;1;2} \right)\) và đi qua điểm \(A\left( {1; - 2; - 1} \right)\). Xét các điểm B, C, D thuộc (S) sao cho AB, AC, AD đôi một vuông góc với nhau. Thể tích của khối tứ diện ABCD có giá trị lớn nhất bằng:

• Diện tích của mặt cầu bán kính R bằng 

• Một người gửi tiết kiệm vào một ngân hàng với lãi suất \(7,5\% \)/năm. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào vốn để tính lãi cho năm tiếp theo. Hỏi sau ít nhất bao nhiêu năm người đó thu được ( cả số tiền gửi ban đầu và lãi) gấp đôi số tiền gửi ban đầu, giả định trong khoảng thời gian này lãi suất không thay đổi và người đó không rút tiền ra ? 

• Cho hàm số\(y = f(x)\) có bảng biến thiên như sau:

  

  Hàm số đã cho nghịch biến trên khoảng nào dưới đây ?

• Ba bạn A, B, C mỗi bạn viết ngẫu nhiên lên bảng một số tự nhiên thuộc đoạn \(\left[ {1;17} \right]\). Xác suất để ba số được viết ra có tổng chia hết cho \(3\) bằng:  

• Nguyên hàm của hàm số \(f\left( x \right) = {x^3} + x\) là: 

• Cho \(\int\limits_{16}^{55} {\frac{{dx}}{{x\sqrt {x + 9} }} = a\ln 2 + b\ln 5 + c\ln 11} \) với a,b,c là các số hữu tỉ. Mệnh đề nào dưới đây đúng? 

• Số phức \( - 3 + 7i\) có phần ảo bằng: 

• Gọi \(S\) là tập hợp tất cả các giá trị nguyên của tham số \(m\) sao cho phương trình \({16^x} - m{.4^{x + 1}} + 5{m^2} - 45 = 0\) có hai nghiệm phân biệt. Hỏi \(S\) có bao nhiêu phần tử? 

• Từ một hộp chứa \(11\) quả cầu màu đỏ và \(4\) quả cầu màu xanh, lấy ngẫu nhiên đồng thời \(3\) quả cầu. Xác suất để lấy được \(3\) quả cầu màu xanh bằng  

• Cho hàm số \(y = \frac{{x - 1}}{{x + 2}}\) có đồ thị (C). Gọi I là giao điểm của hai tiệm cận của (C). Xét tam giác đều ABI có hai đỉnh A, B thuộc (C), đoạn thẳng AB có độ dài bằng:

• Trong không gian Oxyz, đường thẳng \(d:\left\{ \begin{array}{l}x = 2 - t\\y = 1 + 2t\\z = 3 + t\end{array} \right.\) có một vectơ chỉ phương là: 

• Cho \(a > 0,b > 0\) thỏa mãn \({\log _{3a + 2b + 1}}\left( {9{a^2} + {b^2} + 1} \right) + {\log _{6ab + 1}}\left( {3a + 2b + 1} \right) = 2\). Giá trị của \(a + 2b\) bằng: 

• Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB = a, BC = 2a, SA vuông góc với mặt phẳng đáy và SA = a. Khoảng cách giữa hai đường thẳng AC và SB bằng