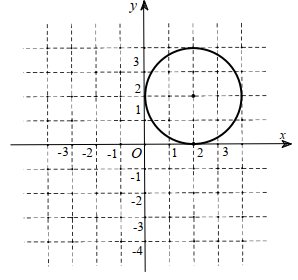
Biết tập hợp tất cả các điểm biểu diễn số phức z là đường tròn cho bởi hình vẽ bên. Hỏi tập hợp tất cả các điểm biểu diễn số phức \(z-3-4 i\) được thể hiện bởi đường tròn trong hình vẽ nào trong bốn hình vẽ dưới đây?

 

Câu hỏi liên quan

• Cho \(z_{1}, z_{2}, z_{3}\)

   là các số phức thỏa mãn \(z_{1}+z_{2}+z_{3}=0 \text { và }\left|z_{1}\right|=\left|z_{2}\right|=\left|z_{3}\right|=1\)

   Khẳng định nào dưới dây là sai?

• Biết rằng phương trình z² + bz + c = 0(b;c thuộc R) có một nghiệm phức là z₁ = 1 + 2i . Khi đó:

• Gọi \(z_{1}, z_{2}, z_{3}\) là các nghiệm của phương trình \(i z^{3}-2 z^{2}+(1-i) z+i=0\) . Biết z_¹ là số thuần ảo. Đặt \(P=\left|z_{2}-z_{3}\right|\) , hãy chọn khẳng định đúng? 

ZUNIA12

• Cho số phức z thỏa mãn điều kiện\(|z|=3\). Biết rằng tập hợp tất cả các điểm biểu diễn số phức \(w=3-2 i+(2-i) z\) là một đường tròn. Hãy tính bán kính của đường tròn đó.

• Tìm nghiệm của phương trình \({\frac{{7 + i}}{{{{(2i\; - 1)}^3}}} = \frac{{3 + i}}{{\;2z + 1}}}\)

• Gọi z₁ là nghiệm có phần ảo âm của phương trình \(z^{2}-4 z+20=0\) . Tìm tọa độ điểm biểu diễn của z₁ . 

• Xét các số phức \(z_{1}, z_{2}\) thỏa mãn \(\left|z_{1}-3 i+5\right|=2 \text { và }\left|i z_{2}-1+2 i\right|=4\). Giá trị lớn nhất của biểu thức \(P=\left|2 i z_{1}+3 z_{2}\right|\) bằng 

• Cho số phức z thỏa mãn \(|z-1-i|=1\), số phức w thỏa mãn \(|\bar{w}-2-3 i|=2\). Giá trị nhỏ nhất của biểu thức \(|z-w|\) bằng

• Cho các số phức z thỏa mãn\(|z|=2\). Biết rằng tập hợp các điểm biểu diễn các số phức \(w=3-2 i+(2-i) z\) là một đường tròn. Tính bán kính r của đường tròn đó.

• Tập hợp điểm biểu diễn số phức  \(\overline z\)  thỏa điều kiện \(|z +1+ 2i|= 1\) nằm trên đường tròn có tâm là:

   

• Tìm số phức z thỏa mãn \((2-i)(1+i)+\bar{z}=4-2 i\)

• Gọi z₁ và z₂ lần lượt là hai nghiệm của phương trình \(z^{2}-4 z+5=0 .\) . Giá trị của biểu thức \(P=\left(z_{1}-2 z_{2}\right) \cdot \overline{z_{2}}-4 z_{1}\) bằng 

• Tính căn bậc hai của số phức \(z=8+6 i\) ra kết quả: 

• Cho hai số phức \(z_{1}=(1-i)(2 i-3), z_{2}=(-i-1)(3+2 i)\) lựa chọn phương án đúng

• Cho số phức z thỏa mãn |z|=1. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức \(P=|z+1|+\left|z^{2}-z+1\right|\) Tính giá trị của M . m .

• Kí hiệu z₁, z₂ là hai nghiệm phức của phương trình z²+z+1 = 0

  Giá trị của biểu  thức P = \(z_1^2 + z_2^2 + {z_1}{z_2}\) bằng:

• Cho số phức thỏa mãn \(z+(1-2 i) \bar{z}=2-4 i\). Tìm môđun của \(w=z^2-z\)

• Cho z₁, z₂ là hai nghiệm của phương trình z² + 2iz + i = 0. Chọn mệnh đề đúng:

• Cho z₁, z₂ là hai nghiệm phức của phương trình 2z₂+1 = 0 (trong đó số phức z1z1 có phần ảo âm). Tính z₁+3z₂.

• Kí hiệu \({z_0}\) là nghiệm phức có phần thực âm và phần ảo dương của phương trình \({z^2} + 2z + 10 = 0\). Trên mặt phẳng tọa độ, điểm nào dưới đây là điểm biểu diễn số phức \({\rm{w}} = {i^{2020}}{z_0}\)?