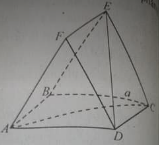
Cho hai tam giác ACD và BCD nằm trên hai mặt phẳng vuông góc với nhau và AC = AD = BC = BD = a, CD = 2x. Tính AB theo a và x?
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai.png)
Gọi H là trung điểm của CD.
Vì tam giác ACD cân tại A và tam giác BCD cân tại B nên \(AH \bot CD\), \(BH \bot CD\).
Ta có .
\(\left. \begin{array}{l} \left( {ACD} \right) \bot \left( {BCD} \right)\\ \left( {ACD} \right) \cap \left( {BCD} \right) = CD\\ \left( {ACD} \right) \supset AH \bot CD \end{array} \right\} \Rightarrow AH \bot \left( {BCD} \right) \Rightarrow AH \bot BH\)
\(\Delta ACD = \Delta BCD\left( {c.c.c} \right) \Rightarrow AH = BH = \sqrt {B{C^2} - C{H^2}} = \sqrt {{a^2} - {x^2}} \)
Tam giác AHB vuông tại H nên
\(AB = \sqrt {A{H^2} + B{H^2}} = \sqrt {2\left( {{a^2} - {x^2}} \right)} \)
Câu hỏi liên quan
-
Cho hình lăng trụ tam giác đều \(ABC.A'B'C'\) có cạnh đáy bằng \(2a\sqrt 3 \) và cạnh bên bằng 2a. Gọi G và G' lần lượt là trọng tâm của hai đáy ABC và A'B'C'. Khẳng định nào sau đây đúng khi nói về AA'G'G?
-
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA ⊥ (ABC) và SA = a/2.
Góc giữa hai mặt phẳng (SAB) và (ABC) bằng:
-
Cho hình chóp tam giác đều S.ABC với SA = 2AB. Góc giữa (SAB) và (ABC) bằng a. Chọn khẳng định đúng trong các khẳng định sau?
-
Cho hai tam giác ACD và BCD nằm trên hai mặt phẳng vuông góc với nhau và AC = AD = BC = BD = a, CD = 2x. Gọi I, J lần lượt là trung điểm của AB và CD. Tính IJ theo a và x?
-
Cho hình chóp S.ABCD có hai mặt bên (SAB) và (SAC) vuông góc với mặt phẳng (ABC), tam giác ABC vuông cân ở A và có đường cao AH \(\left( {H \in BC} \right)\). Gọi O là hình chiếu vuông góc của A lên (SBC). Khẳng định nào sau đây sai ?
-
Cho tứ diện ABCD có: AB = AC = AD, góc BAC bằng góc BAD bằng 60o. Gọi M và N lần lượt là trung điểm của AB và CD.
Góc giữa hai mặt phẳng (ACD) và (BCD) là:
-
Cho tứ diện ABCD có: AB = AC = AD, góc BAC bằng góc BAD bằng 60o60o. Gọi M và N lần lượt là trung điểm của AB và CD.
Mặt phẳng (BCD) vuông góc với mặt phẳng
-
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và có SA = SB = SC = a. Góc giữa hai mặt phẳng (SBD) và (ABCD) bằng
-
Cho hai tam giác ACD và BCD nằm trên hai mặt phẳng vuông góc với nhau và \(AC = AD = BC = BD = a;CD = 2x\). Với giá trị nào của x thì hai mặt phẳng (ABC) và (ABD) vuông góc.
-
Cho tứ diện đều ABCD. Gọi M là trung điểm cạnh BC (tham khảo hình vẽ bên). Giá trị cô-sin của góc giữa hai đường thẳng AB và DM bằng
-
Cho hình chóp tứ giác S.ABCD, có đáy ABCD là hình thoi tâm I cạnh bằng a và góc \(\widehat A = {60^0}\), cạnh \(SC = \frac{{a\sqrt 6 }}{2}\) và SC vuông góc với mặt phẳng (ABCD). Trong tam giác SCA kẻ \(IK \bot SA\) tại K. Tính độ dài IK được
-
Cho hình chóp S.ABC có SA = SB = SC = AB = AC = 1, \(B C=\sqrt{2}\). Tính góc giữa hai đường thẳng AB, SC
-
Cho hình lăng trụ ABCD.A'B'C'D' có đáy ABCD là hình thoi, AC = 2a. Các cạnh bên vuông góc với đáy và AA' = a. Khẳng định nào sau đây sai ?
-
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O. Biết \(SO \bot \left( {ABCD} \right),SO = a\sqrt 3 \) và đường tròn nội tiếp ABCD có bán kính bằng a. Tính góc hợp bởi mỗi mặt bên với đáy.
-
Cho tứ diện OABC có OA,OB,OC đôi một vuông góc với nhau và OA=OB=OC. Gọi M là trung điểm của BC (tham khảo hình vẽ bên). Góc giữa hai đường thẳng OM và AB bằng
-
Cho hình chóp tứ giác S.ABCD, có đáy ABCD là hình thoi tâm I cạnh bằng a và góc \(\widehat A = {60^0}\), cạnh \(SC = \frac{{a\sqrt 6 }}{2}\) và SC vuông góc với mặt phẳng (ABCD). Trong tam giác SAC kẻ \(IK \bot SA\) tại K. Tính số đo góc \(\widehat {{\rm{BKD}}}\).
-
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và SA = SB = SC = a.
Mặt phẳng (ABCD) vuông góc với mặt phẳng:
-
Cho hình chóp tứ giác đều có cạnh đáy bằng \(a\sqrt 2 \) và chiều cao bằng \(\frac{{a\sqrt 2 }}{2}\). Tính số đo của góc giữa mặt bên và mặt đáy.
-
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, cạnh bên SA vuông góc với đáy, SA = a. Gọi M là trung điểm của SB. Góc giữa AM và BD bằng
-
Cho hình chóp tứ giác đều S.ABCD, có đáy ABCD là hình vuông tâm O. Các cạnh bên và các cạnh đáy đều bằng A. Gọi M là trung điểm SC. Góc giữa hai mặt phẳng (MBD) và (ABCD) bằng:
