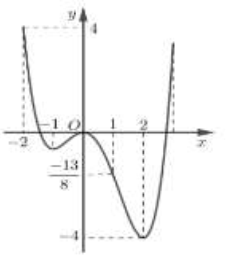
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình dưới đây. Tìm giá trị lớn nhất của hàm số \(g\left( x \right) = f\left( {4x – {x^2}} \right) + \frac{1}{3}{x^3} – 3{x^2} + 8x + \frac{1}{3}\) trên đoạn \(\left[ {1\,;\,3} \right]\).
.png)
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai\(g’\left( x \right) = \left( {4 – 2x} \right)f’\left( {4x – {x^2}} \right) + {x^2} – 6x + 8 = \left( {2 – x} \right)\left[ {2f’\left( {4x – {x^2}} \right) + 4 – x} \right]\)
Với \(x \in \left[ {1\,;\,3} \right]\) thì 4 – x > 0; \(3 \le 4x – {x^2} \le 4\) nên \(f’\left( {4x – {x^2}} \right) > 0\)
Suy ra \(2f’\left( {4x – {x^2}} \right) + 4 – x > 0, \forall x \in \left[ {1\,;\,3} \right]\)
Bảng biến thiên
.png)
Suy ra \(\mathop {\max }\limits_{\left[ {1\,;\,3} \right]} g\left( x \right) = g\left( 2 \right) = f\left( 4 \right) + 7 = 12\)
.PNG)