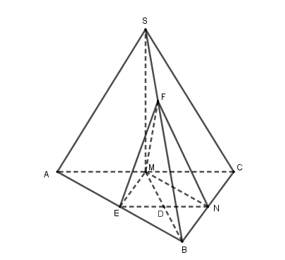
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân đỉnh B, AB = 4,SA = SB = SC = 12 . Gọi M, N, E lần lượt là trung điểm AC, BC, AB. Trên cạnh SB lấy điểm F sao cho \( \frac{{BF}}{{BS}} = \frac{2}{3}\) Thể tích khối tứ diện (MNEF ) bằng
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiGọi D là giao điểm của MB và EN thì D là trung điểm của MB.
Ta có: \( {V_{MNEF}} = {V_{M.NEF}} = \frac{1}{3}{S_{NEF}}.d\left( {M,\left( {NEF} \right)} \right)\)
Do D là trung điểm của MB và MB cắt (EFN) tại D nên \( d\left( {M,\left( {NEF} \right)} \right) = d\left( {B,\left( {NEF} \right)} \right)\))
\( \Rightarrow {V_{MNEF}} = \frac{1}{3}{S_{NEF}}.d\left( {B,\left( {NEF} \right)} \right)\)
Mà
\(\begin{array}{l} \frac{{{V_{B.NEF}}}}{{{V_{B.CAS}}}} = \frac{{BN}}{{BC}}.\frac{{BE}}{{BA}}.\frac{{BF}}{{BS}} = \frac{1}{2}.\frac{1}{2}.\frac{2}{3} = \frac{1}{6}\\ \Rightarrow {V_{B.NEF}} = \frac{1}{6}{V_{B.CAS}} = \frac{1}{6}{V_{S.ABC}} \end{array}\)
Vì SA=SB=SC nên SS nằm trên trục đường tròn ngoại tiếp tam giác ABC.
Mà ABC vuông cân nên M là tâm đường tròn ngoại tiếp tam giác. Do đó SM⊥(ABC)
Diện tích tam giác ABC là \( {S_{ABC}} = \frac{1}{2}AB.BC = \frac{1}{2}.4.4 = 8\)
Tam giác ABC vuông cân tại B nên
\(\begin{array}{*{20}{l}} {AC = \sqrt {A{B^2} + B{C^2}} }\\ { = \sqrt {{4^2} + {4^2}} = 4\sqrt 2 }\\ { \Rightarrow AM = \frac{1}{2}AC = \frac{1}{2}.4\sqrt 2 = 2\sqrt 2 } \end{array}\)
Tam giác SMA vuông tại M nên theo Pitago ta có:
\( SM = \sqrt {S{A^2} - A{M^2}} = \sqrt {{{12}^2} - {{\left( {2\sqrt 2 } \right)}^2}} = 2\sqrt {34} \)
Thể tích khối chóp S.ABC là:
\( {V_{S.ABC}} = \frac{1}{3}{S_{ABC}}.SM = \frac{1}{3}.8.2\sqrt {34} = \frac{{16\sqrt {34} }}{3}\)
Thể tích khối tứ diện MNEF là:
\( {V_{MNEF}} = \frac{1}{6}.{V_{S.ABC}} = \frac{1}{6}.\frac{{16\sqrt {34} }}{3} = \frac{{8\sqrt {34} }}{9}\)
Đáp án cần chọn là: A