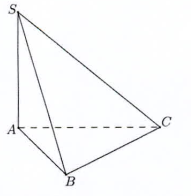
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại đỉnh A và AB = AC, SA = SB = SC = 3a. Góc giữa mặt phẳng (SAB) và mặt phẳng (ABC) là 60o. Gọi G là trọng tâm của tam giác SAB. Thể tích khối chóp S.GBC là:
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo saiGọi H là chân đường vuông góc hạ từ đỉnh S lên mặt phẳng (ABC), khi đó ta chứng minh được H là trung điểm của BC. Gọi M là trung điểm của AB khi đó từ giả thiết ta có:
Đặt AB = x ta tính được:
\(\begin{array}{l}
\left( {\widehat {\left( {SAB} \right),\left( {ABCD} \right)}} \right) = \widehat {SMH} = {60^0}\\
x = \frac{{6a}}{{\sqrt 5 }} \Rightarrow {V_{S.GBC}} = \frac{2}{3}{V_{S.ABC}} = \frac{{{a^3}\sqrt 3 }}{{36}} = \frac{{6{a^3}\sqrt {15} }}{{25}}
\end{array}\)
ADMICRO
YOMEDIA
ZUNIA9