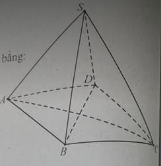
Cho hình chóp tam giác đều S.ABC có độ dài cạnh đáy bằng a, cạnh bên bằng \(a\sqrt 3 \). Gọi H là trọng tâm tam giác ABC, \({d_1}\) khoảng cách từ A đến mặt phẳng \(\left( {SBC} \right), {d_2}\) khoảng cách từ H đến mặt phẳng \(\left( {SBC} \right)\). Khi đó \({d_1} + {d_2}\) có giá trị bằng
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai
Vì H là trọng tâm tam giác ABC nên \(d\left( {A,\left( {SBC} \right)} \right) = 3d\left( {H,\left( {SBC} \right)} \right) \Rightarrow {d_2} = \frac{1}{3}{d_1}\).
Kẻ \(AI \bot SM \Rightarrow AI \bot \left( {SBC} \right) \Rightarrow {d_1} = AI = \frac{{2{S_{\Delta SAM}}}}{{SM}}\).
Ta có
\(AM = \frac{{a\sqrt 3 }}{2};AH = \frac{{a\sqrt 3 }}{3};SM = \sqrt {{{\left( {a\sqrt 3 } \right)}^2} – {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt {11} }}{2};SH = \sqrt {{{\left( {a\sqrt 3 } \right)}^2} – {{\left( {\frac{{a\sqrt 3 }}{3}} \right)}^2}} = \frac{{a\sqrt {24} }}{3}\).
\({S_{\Delta SAM}} = \frac{1}{2}AM.SH = \frac{1}{2}.\frac{{a\sqrt 3 }}{2}.\frac{{a\sqrt {24} }}{3} = \frac{{\sqrt 2 }}{2}{a^2} \Rightarrow {d_1} = \frac{{{a^2}\sqrt 2 }}{{\frac{{a\sqrt {11} }}{2}}} = \frac{{2\sqrt {22} a}}{{11}}\).
Vậy \({d_1} + {d_2} = \frac{4}{3}{d_1} = \frac{{8\sqrt {22} }}{{33}}a\).