Cho lăng trụ đứng \(A B C \cdot A^{\prime} B^{\prime} C^{\prime}\) có đáy ABC là tam giác vuông tại B và B A=B C=1. Cạnh A'B tạo với mặt đáy (ABC) góc \(60^{\circ}\) Thể tích của khối lăng trụ đã cho bằng
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo sai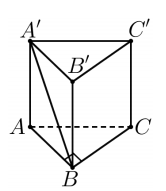
Xác định: \(60^{\circ}=\left(\widehat{A^{\prime} B,(A B C)}\right)=\left(\widehat{A^{\prime} B, A B}\right)=\widehat{A^{\prime} B A}\)
Tam giác vuông A'AB, ta có \(A A^{\prime}=A B \cdot \tan \widehat{A^{\prime} B A}=\sqrt{3}\)
Diện tích tam giác:\(S_{\Delta A B C}=\frac{1}{2} B A \cdot B C=\frac{1}{2}\)
Vậy \(V=S_{A A B C} \cdot A A^{\prime}=\frac{\sqrt{3}}{2}\)
ADMICRO
YOMEDIA
ZUNIA9











