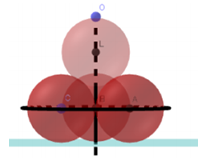
Cho mặt cầu \(S\left( O;R \right),A\) là một điểm ở trên mặt cầu \(\left( S \right)\) và \(\left( P \right)\) là mặt phẳng đi qua A sao cho góc giữa OA và (P) bằng \({{60}^{0}}.\) Diện tích của đường tròn giao tuyến bằng:

Bạn Nam cao 1,8m tham gia trò chơi nhà bóng. Bạn Nam phải đứng thẳng trong quả bóng hình cầu và lăn trên cỏ. Để Nam có thể đứng được trong quả bóng thì Nam phải chọn quả bóng có thể tích ít nhất là bao nhiêu trong các kết quả sau:

Trong không gian \(Oxyz\), Cho mặt cầu \(\left( S \right)3{x^2} + 3{y^2} + 3{z^2} + 6x + 12y – 18z – 3 = 0\). Tâm của \((S)\) có tọa độ là

Diện tích hình tròn lớn của một hình cầu \(p.\) Một mặt phẳng \(\left( \alpha  \right)\) cắt hình cầu theo một hình tròn có diện tích là \(\frac{p}{2}.\) Khoảng cách từ tâm mặt cầu đến mặt phẳng \(\left( \alpha  \right)\) bằng:

Với điều kiện nào của m thì mặt phẳng cong sau là mặt cầu? 

\(\left( S \right):{x^2} + {y^2} + {z^2} + 2\left( {3 - m} \right)x - 3\left( {m + 1} \right)y - 2mz + 2{m^2} + 7 = 0\)

Một nóc tòa nhà cao tầng có dạng hình nón. Người ta muốn xây một bể nước có dạng một hình trụ nội tiếp trong hình nón để chứa nước (như hình vẽ minh họa). Cho biết SO=h;OB=R;OH=x₀<x<h. Tìm thể tích lớn nhất của hình trụ.

Điều kiện để \(\left( S \right):{x^2} + {y^2} + {z^2} + Ax + By + Cz + D = 0\) là một mặt cầu là:

Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (ABC), tam giác ABC vuông tại B có cạnh AB = 3 , BC = 4 và góc giữa DC và mặt phẳng (ABC) bằng 45⁰. Tính thể tích mặt cầu ngoại tiếp tứ diện.

Một bình đựng nước dạng hình nón (không có đáy), đựng đầy nước. Người ta thả vào đó một khối cầu có đường kính bằng chiều cao của bình nước và đo được thể tích nước tràn ra ngoài là  18π(dm³)  . Biết rằng khối cầu tiếp xúc với tất cả các đường sinh của hình nón và đúng một nửa của khối cầu chìm trong nước (hình bên). Tính thể tích V của nước còn  lại trong bình.

Trong không gian Oxyz, mặt cầu \(\left( S \right)\) có tâm là điểm \(I\left( {1\,;\, – 1\,;\,2} \right)\) và cắt mặt phẳng \(\left( P \right):2x – 2y + z + 3 = 0\) theo một đường tròn có bán kính bằng 4 có phương trình là

Cho lăng trụ đứng \(ABC.A'B'C'\) có đáy là tam giác đều cạnh \(a\). Mặt phẳng \(\left( AB'C' \right)\) tạo với mặt đáy góc \({{60}^{0}}\) và điểm \(G\) là trọng tâm tam giác \(ABC\). Bán kính mặt cầu ngoại tiếp khối chóp \(G.A'B'C'\) bằng:

Cho hình hộp chữ nhật ABCD.A'B'C'D'  có AB = a, AD = 2a, AA' = 3a . Thể tích khối cầu ngoại tiếp hình hộp chữ nhật ABCD.A'B'C'D' là

Cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA vuông góc với mặt phẳng đáy. Khi đó tâm mặt cầu ngoại tiếp hình chóp là điểm nào?

Trong không gian với hệ tọa độ Oxyz, \(A(-3 ; 4 ; 2), B(-5 ; 6 ; 2), C(-10 ; 17 ;-7)\). Viết phương trình mặt cầu tâm C bán kính AB . 

Cho mặt cầu (S) tâm O bán kính R và một đường thẳng d. Kí hiệu h là khoảng cách từ O đến đường thẳng d. Đường thẳng d có điểm chung với mặt cầu (S) nếu và chỉ nếu:

Cho mặt cầu \(\left( S \right):{x^2} + {y^2} + {z^2} - 2x + 4y - 2z - 3 = 0\). cắt hai mặt phẳng (P):x−2y+z=0 và (Q):x−z−2=0 theo các đường tròn giao tuyến với bán kính r₁ và r₂. Khi đó tỉ số \(\frac{{{r_1}}}{{{r_2}}}\) bằng:

Nếu tăng bán kính của mặt cầu lên 4 lần thì diện tích mặt cầu tăng lên bao nhiêu lần?

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a, AD = 2a, SA vuông góc (ABCD)  và SA = 2a. Tính thể tích khối cầu ngoại tiếp hình chóp S.ABCD 

Trong không gian \(Oxyz,\) cho mặt cầu \((S):{x^2} + {y^2} + {z^2} – 2y + 4z + 2 = 0.\) Độ dài đường kính của mặt cầu \((S)\) bằng

Trong không gian với hệ toạ độ Oxyz, cho mặt cầu \(\left( S \right):\,{\left( {x – 1} \right)^2} + {\left( {y – 3} \right)^2} + {\left( {z – 2} \right)^2} = 4\). Gọi \(N\left( {{x_0};{y_0};{z_0}} \right)\) là điểm thuộc \(\left( S \right)\) sao cho khoảng cách từ điểm N đến mặt phẳng \(\left( {Oxz} \right)\) lớn nhất. Giá trị của biểu thức \(P = {x_0} + {y_0} + {z_0}\) bằng

Tập hợp các điểm cách đều hai đầu mút của đoạn thẳng là: