Cho tam giác ABC có A là góc nhọn và các đường cao là \(A A^{\prime}, B B^{\prime}, C C^{\prime}\). Gọi H là trực tâm tam giác ABC và H ′ là điểm đối xứng của H qua BC. Tứ giác nào sau đây là tứ giác nội tiếp ?
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai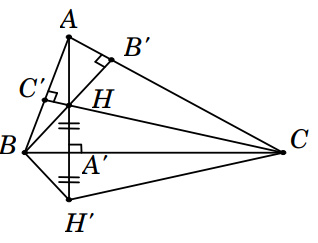
Vì H ′ đối xứng với H qua BC suy ra \(\widehat{B H C}=\widehat{B H^{\prime} C}\) . Mặt khác \(\widehat{B H C}=\widehat{B^{\prime} H C^{\prime}}\)(Hai góc đối đỉnh)
Suy ra \(\widehat{B H^{\prime} C}=\widehat{B^{\prime} H C^{\prime}}\,\,\,\,\,(1)\)
Ta có \(\left\{\begin{array}{l} B B^{\prime} \perp A C \\ C C^{\prime} \perp A B \end{array} \Rightarrow \widehat{A C^{\prime} H}=\widehat{A B^{\prime} H}=90^{\circ}\right.\)
Vậy tứ giác AB'HC' là tứ giác nội tiếp.
Suy ra \(\widehat{B^{\prime} A C^{\prime}}+\widehat{B^{\prime} H C^{\prime}}=180^{0}\,\,\,\,\,(2)\)
Từ (1) và (2) suy ra \(\widehat{B H^{\prime} C}+\widehat{B A C}=180^{\circ}\)
Vậy tứ giác ABH'C là tứ giác nội tiếp.
Câu hỏi liên quan
-
Trong mặt phẳng với hệ trục tọa độ Oxy , cho phép đối xứng trục Ox , với M(x ; y) ; gọi M' là ảnh của M qua phép đối xứng trục Ox . Khi đó tọa độ điểm M' là:
-
Trong mặt phẳng cho hai đường thẳng a và b tạo với nhau góc 60o. Có bao nhiêu phép đối xứng trục biến a thành b.
-
Tìm mệnh đề sai trong các mệnh đề sau:
-
Hình gồm hai đường thẳng d và d ' vuông góc với nhau có mấy trục đối xứng?
-
Trong mặt phẳng Oxy cho đường thẳng d có phương trình : x - 2y + 4 = 0. Phép đối xứng trục Ox biến d thành d’ có phương trình:
-
Trong mặt phẳng Oxy , cho parabol (P) có phương trình \(x^{2}=4 y\) . Hỏi Parabol nào trong các Parabol sau là ảnh của P qua phép đối xứng trục Ox ?
-
Trong mặt phẳng tọa độ Oxy cho đường thẳng ∆ có phương trình \(5 x+y-3=0\) Đường thẳng đối xứng của ∆ qua trục tung có phương trình là:
-
Trong các chữ cái dưới đây, chữ cái có trục đối xứng?
.png)
-
Trong mặt phẳng Oxy , cho điểm M ( 2;3) . Hỏi M là ảnh của điểm nào trong các điểm sau qua phép đối xứng trụcOy ?
-
Trong mặt phẳng tọa độ Oxy qua phép đối xứng trục Oy , điểm A(3;5) biến thành điểm nào trong các điểm sau?
-
Trong mặt phẳng Oxy cho đường tròn (C) có phương trình: \({x^2}\; + \;{y^2}\; - \;4x\; + \;5y\; + \;1\; = \;0\). Phép đối xứng trục Oy biến (C) thành (C’) có phương trình:
-
Trong các mệnh đề sau mệnh đề nào đúng?
-
Xem các chữ cái in hoa A, B, C, D, X, Y như những hình. Khẳng định nào sau đây đúng?
-
Giả sử rằng qua phép đối xứng trục \(\mathrm{Đ}_{a}\) ( a là trục đối xứng), đường thẳng d biến thành đường thẳng d' . Hãy chọn câu sai trong các câu sau:
-
Trong mặt phẳng Oxy cho parabol (P) có phương trình: \(y\; = \;6{x^2}\; - \;3x\; + \;13\). Phép đối xứng trục Ox biến (P) thành (P’) có phương trình:
-
Trong mặt phẳng tọa độ Oxy cho đường thẳng d có phương trình \(3 x+y-1=0\) . Xét phép đối xứng trục \(\Delta: 2 x-y+1=0\) , đường thẳng d biến thành đường thẳng d ' có phương trình là:
-
Trong mặt phẳng, hình nào sau đây có trục đối xứng?
-
Tam giác đều có bao nhiêu trục đối xứng?
-
Cho hai đường thẳng song song a và b , một đường thẳng c vuông góc với chúng. Có bao nhiêu phép đối xứng trục biến mỗi đường thẳng đó thành chính nó?
-
Trong các mệnh đề sau, mệnh đề nào đúng?
