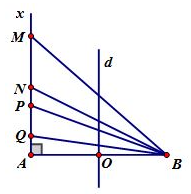
Ở mặt chất lỏng có 2 nguồn kết hợp đặt tại A và B dao động điều hòa, cùng pha theo phương thẳng đứng. Ax là nửa đường thẳng nằm ở mặt chất lỏng và vuông góc với AB. Trên Ax có những điểm mà các phần tử ở đó dao động với biên độ cực đại, trong đó M là điểm xa A nhất, N là điểm kế tiếp với M, P là điểm kế tiếp với N và Q là điểm gần A nhất. Biết MN = 22,25 cm, NP = 8,75 cm. Độ dài đoạn QA gần nhất với giá trị nào sau đây?

A. 1,2cm

B. 4,2cm

C. 2,1cm

D. 3,1cm

Suy nghĩ và trả lời câu hỏi trước khi xem đáp án

Môn: Vật Lý Lớp 12

Chủ đề: Sóng cơ và sóng âm

Bài: Sóng cơ và sự truyền sóng cơ

Lời giải:

Báo sai

+ Ta thấy trên nửa đường thẳng kẻ từ A vuông góc với AB có 4 điểm theo thứ tự M,N,P,Q dao động với biên độ cực đại

=> Nên AB có 9 điểm dao động với biên độ cực đại với: \( - 4 \le k \le 4\left( {{d_2} - {d_1} = k\lambda } \right)\)

Cực đại M,N,P,Q ứng với k=1,2,3,4

+ Đặt AB=a

Tại C trên Ax là điểm dao động với biên độ cực đại:

\(\begin{array}{l} CB - CA = k\lambda \left( * \right)\\ \begin{array}{*{20}{l}} {C{B^2} - C{A^2} = {a^2}}\\ { \to \left( {CB - CA} \right)\left( {CB + CA} \right) = {a^2}}\\ { \to CB + CA = \frac{{{a^2}}}{{k\lambda }}\left( { * * } \right)} \end{array} \end{array}\)

Từ (∗) và (∗∗) ta suy ra \(CA = \frac{{{a^2}}}{{2k\lambda }} - \frac{{k\lambda }}{2}\)

- Tại M ứng với k=1: \( MA = \frac{{{a^2}}}{{2\lambda }} - \frac{\lambda }{2}\left( 1 \right)\)

- Tại N ứng với k=2 \( NA = \frac{{{a^2}}}{{2.2\lambda }} - \frac{{2\lambda }}{2} = \frac{{{a^2}}}{{4\lambda }} - \lambda \left( 2 \right)\)

- Tại P ứng với k=3 \( PA = \frac{{{a^2}}}{{2.3\lambda }} - \frac{{3\lambda }}{2} = \frac{{{a^2}}}{{6\lambda }} - \frac{{3\lambda }}{2}\left( 3 \right)\)

- Tại Q ứng với k=4 \( QA = \frac{{{a^2}}}{{2.4\lambda }} - \frac{{4\lambda }}{2} = \frac{{{a^2}}}{{8\lambda }} - 2\lambda \left( 4 \right)\)

Lấy (1)−(2) ta được: \( MN = MA - NA = \frac{{{a^2}}}{{4\lambda }} + \frac{\lambda }{2} = 22,25cm\left( 5 \right)\)

Lấy (2)−(3) ta được \( NP = NA - PA = \frac{{{a^2}}}{{12\lambda }} + \frac{\lambda }{2} = 8,75cm\left( 6 \right)\)

Lấy 3.(6)−(5) ta được:

\(\begin{array}{*{20}{l}} {3\left( {\frac{{{a^2}}}{{12\lambda }} + \frac{\lambda }{2}} \right) - \left( {\frac{{{a^2}}}{4} + \frac{\lambda }{2}} \right) = 3.8,75 - 22,25}\\ { \to \lambda = 4cm} \end{array}\)

Lấy (5)−(6) ta được: \( \frac{{{a^2}}}{{6\lambda }} = 22,25 - 8,75 = 13,5cm \to \frac{{{a^2}}}{\lambda } = 81cm\)

Thay \(\left\{ \begin{array}{l} \lambda = 4cm\\ \frac{{{a^2}}}{\lambda } = 81cm \end{array} \right.\) vào (4) ta được: \( QA = \frac{{{a^2}}}{{8\lambda }} - 2\lambda = \frac{{81}}{8} - 2.4 = 2,125cm\)