Phương trình \(\sin ^{6} x+\cos ^{6} x+3 \sin x \cos x-m+2=0\) có nghiệm khi \(m \in[a ; b]\) thì tích a.b bằng:
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo sai\(\begin{aligned} &\sin ^{6} x+\cos ^{6} x+3 \sin x \cdot \cos x-m+2=0\\ &\Leftrightarrow 1-\frac{3}{4} \sin ^{2} 2 x+\frac{3}{2} \sin 2 x-m+2=0\\ &\Leftrightarrow 4 m=-3 \sin ^{2} 2 x+6 \sin 2 x+12 \end{aligned}\)
Đặt \(t=\sin 2 x, t \in[-1 ; 1] . \text { Xét } f(t)=-3 t^{2}+6 t+12 \text { trên }[-1 ; 1]\)
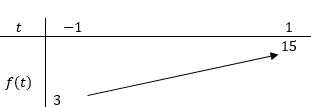
Suy ra (*) có nghiệm \(\Leftrightarrow 3 \leq 4 m \leq 15 \Leftrightarrow \frac{3}{4} \leq m \leq \frac{15}{4}\)
Vậy \(a b=\frac{75}{16}\)
ADMICRO
YOMEDIA
ZUNIA9











