Trắc nghiệm Cực trị của hàm số Toán Lớp 12
-
Câu 1:
Tìm số các giá trị nguyên của tham số m để hàm số \(y = x⁴ + 2(m² - m - 6)x² + m -1 \)có ba điểm cực trị
-
Câu 2:
Cho hàm số \( y = mx⁴ + (2m +1)x² +1\). Tìm tất cả các giá trị thực của tham số m để hàm số có đúng một điểm cực tiểu.
-
Câu 3:
Cho hàm số \(y = mx⁴ - x² +1\). Tập hợp các số thực m để hàm số đã cho có đúng một điểm cực trị là
-
Câu 4:
Tìm tất cả các giá trị của tham số m để hàm số \(y = - \frac{x^3}{3} + mx² - 2mx +1 \) có cực đại tại x=1
-
Câu 5:
Có bao nhiêu giá trị nguyên ucra tham số m để hàm số \(y = x⁸ + (m - 2) x⁵ - (m² - 4) x⁴ + 1\) đạt cực tiểu tại x=0
-
Câu 6:
Có bao nhiêu số thực m để hàm số \(y = \frac{1}{3} x³ - mx² + (m² - m +1) x +1 \) đạt cực đại tại x=1
-
Câu 7:
Có bao nhiêu giá trị nguyên của tham số m để hàm số \(y = x⁸ + (m -1)x⁵ - (m² -1)x⁴ +1 \) đạt cực tiểu taị x=0
-
Câu 8:
Tìm các giá trị thực của tham số m để hàm số \(y = x³ - 3x² + m x + 1\) đạt cực đại tại x = 2
-
Câu 9:
Tìm m để hàm số \(y = x³ - 2mx² + mx + 1 \) đạt cực tiểu tại x=1
-
Câu 10:
Tìm giá trị thực của tham số m để hàm số \(y = \frac{1}{3} x³ - mx² + (m² - 4) x + 3\) đạt cực đại tại x = 3
-
Câu 11:
Cho hàm số y = f ( x) có đạo hàm trên \(\mathbb{R}\) và \(f '( x) = ( x -1)( x - 2)^2 ( x + 3)\) . Số điểm cực trị của hàm số đã cho là
-
Câu 12:
Cho hàm số y = f ( x) có đạo hàm \(f '( x) = x (x² + 2x)^3 (x² -\sqrt 2 )\,\,\forall x\in\mathbb{R}\) . Số điểm cực trị của hàm số là
-
Câu 13:
Cho hàm số y=f(x) có đạo hàm \(f '( x ) = ( x - 2)( x² - 3)( x⁴ - 9)\). Số điểm cực trị của hàm số y=f(x) là?
-
Câu 14:
Cho hàm số F(x) là một nguyên hàm của hàm số \(f ( x ) = 2019x ( x² - 4)( x² - 3x + 2)\). Khi đó số điểm cực trị của hàm số F(x) là
-
Câu 15:
Hàm số y=f(x) có đạo hàm \(f'(x)= ( x -1)( x - 2)...( x - 2019) \,\,\,\forall x\in \mathbb{R} \). Hàm số y=f(x) có tất cả bao nhiêu điểm cực tiểu?
-
Câu 16:
Cho hàm số \(y = ax³ + bx² + cx + d\,\, (a,b, c, d \mathbb{R}) \)có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số này là
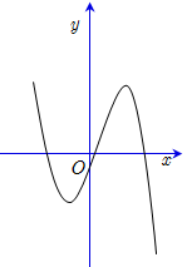
-
Câu 17:
Cho hàm số f (x) có bảng biến thiên như sau:
.png)
hàm số đã cho đạt cực tiểu tại
-
Câu 18:
Cho hàm số y = f (x) có bảng biến thiên như sau
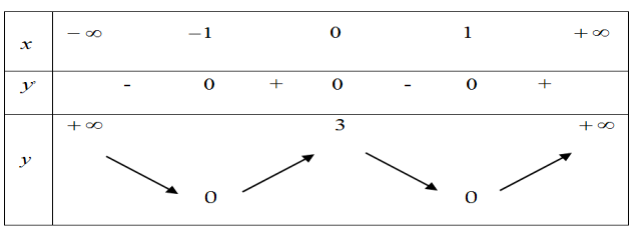
Mệnh đề nào dưới đây sai?
-
Câu 19:
Cho hàm số \(y = ax⁴ + bx² + c\,(a,b,c\in\mathbb{R})\) có đồ thị như hình vẽ bên.
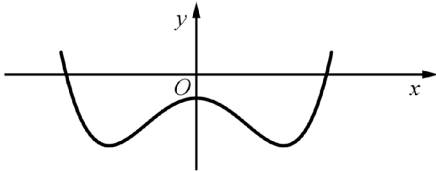
Số điểm cực trị của hàm số đã cho là?
-
Câu 20:
Cho hàm số y= f( x) có bảng biến thiên như sau
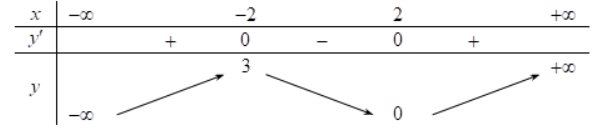
Tìm giá trị cực đại và giá trị cực tiểu của hàm số đã cho.
-
Câu 21:
Cho hàm số có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số đã cho là:
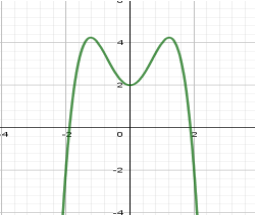
-
Câu 22:
Cho hàm số y=f(x) có bảng biến thiên như sau:
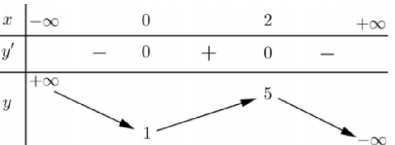
Giá trị cực đại của hàm số đã cho là:
-
Câu 23:
Cho hàm số y = f (x) có bảng biến thiên như sau:
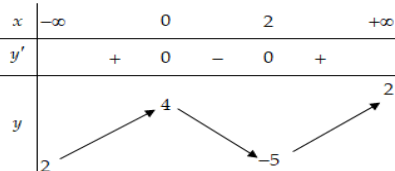
Mênh đề nào dưới đây đúng?
-
Câu 24:
Cho hàm số có bảng biến thiên ở hình bên. Khẳng định nào sau đây là khẳng định sai?
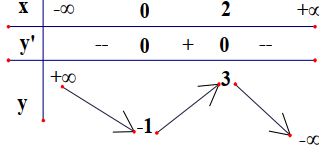
-
Câu 25:
Cho hàm số y = f(x) xác định, liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình vẽ. Khẳng định nào là sai?
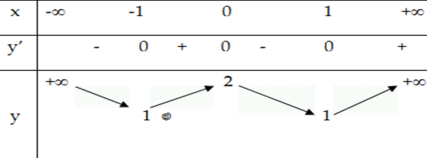
-
Câu 26:
Hàm số y = f ( x) liên tục trên \(\mathbb{R}\) và có bảng biến thiên dưới đây. Khẳng định nào sau đây là đúng?
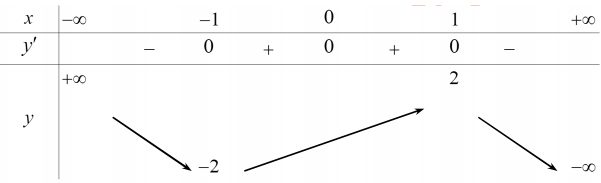
-
Câu 27:
Cho hàm số y = f (x) xác định, liên tục trên đoạn [-2;2] và có đồ thị là đường cong trong hình vẽ bên. Cực tiểu của hàm số f(x) là giá trị nào nào dưới đây?
.png)
-
Câu 28:
Cho hàm số y = f (x) xác định, liên tục trên \(\mathbb{R}\) và có đồ thị như hình bên. Tìm số điểm cực trị của hàm số y =|f(|x|)|
-
Câu 29:
Cho hàm số y = f (x) xác định, liên tục trên \(\mathbb{R}\) và có đồ thị như hình bên. Tìm số điểm cực trị của hàm số y=f(|x|).
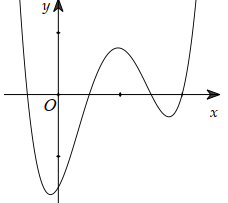
-
Câu 30:
Cho hàm số y = f(x) xác định, liên tục trên \(\mathbb{R}\) và có đồ thị như hình bên. Tìm số điểm cực trị của hàm số y=|f(x)|
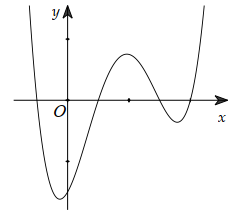
-
Câu 31:
Cho hàm số y = f (x) xác định, liên tục trên \(\mathbb{R}\) và có đồ thị như hình bên. Tìm số điểm cực trị của hàm số y = f( |x|)
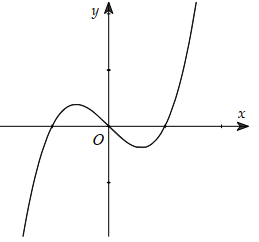
-
Câu 32:
Cho hàm số y = f (x) xác định, liên tục trên \(\mathbb{R}\) và có đồ thị như hình bên. Tìm số điểm cực trị của hàm số y =|f(x)|.
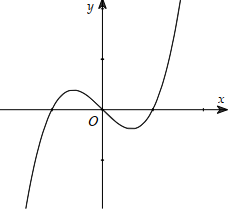
-
Câu 33:
Cho hàm số y = f (x) xác định, liên tục trên \(\mathbb{R}\) và hàm số đạo hàm f '(x) của f (x) có đồ thị như hình bên. Tìm số điểm cực trị của hàm số.
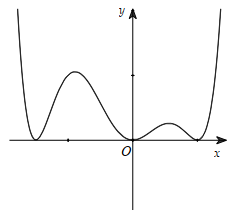
-
Câu 34:
Cho hàm số y = f (x) xác định, liên tục trên đoạn [-2;2] và có đồ thị là đường cong trong hình vẽ bên. Cực đại của hàm số f (x) là giá trị nào nào dưới đây?
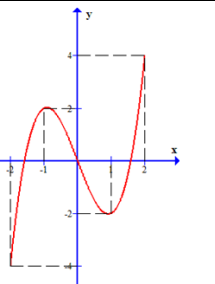
-
Câu 35:
Cho hàm số
y = f (x) xác định, liên tục trên \(\mathbb{R}\)và hàm số đạo hàm f '(x) của f (x) có đồ thị như hình bên. Tìm số điểm cực trị của hàm số y = f(x)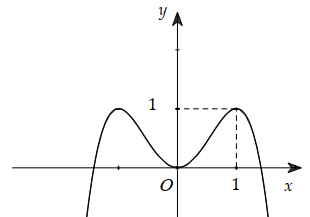
-
Câu 36:
Cho hàm số y = f (x) xác định, liên tục trên \(\mathbb{R}\)và hàm số đạo hàm f '(x) của f (x) có đồ thị như hình bên. Tìm số điểm cực trị của hàm số y = f (x).
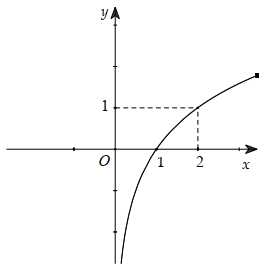
-
Câu 37:
Cho hàm số y = f (x) xác định, liên tục trên đoạn [-2;2] và có đồ thị là đường cong trong hình vẽ bên. Hàm số f (x) đạt cực tiểu tại điểm nào dưới đây?
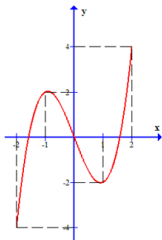
-
Câu 38:
Cho hàm số y = f (x) xác định, liên tục trên đoạn [-2;2] và có đồ thị là đường cong trong hình vẽ bên. Hàm số f (x) đạt cực đại tại điểm nào dưới đây?
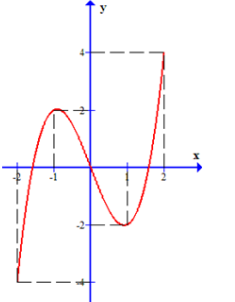
-
Câu 39:
Cho đồ thị hàm số y=f(x) xác địn, liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ. Khẳng định nào sau đây đúng?
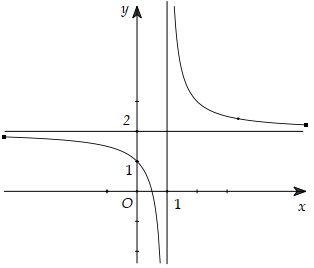
-
Câu 40:
Cho hàm số y=f(x) xác định, liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ:
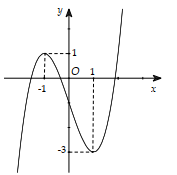
Khẳng định nào sau đây đúng?
-
Câu 41:
Cho hàm số y = f (x) có bảng xét dấu đạo hàm như sau

Khẳng định nào sau đây sai?
-
Câu 42:
Cho hàm số y = f (x) có bảng xét dấu đạo hàm như sau
.png)
Khẳng định nào sau đây đúng?
-
Câu 43:
Cho hàm số y=f(x) xác định, liên tục trên \(\mathbb{R}\backslash{\{-1\}}\) và có bảng biến thiên sau:
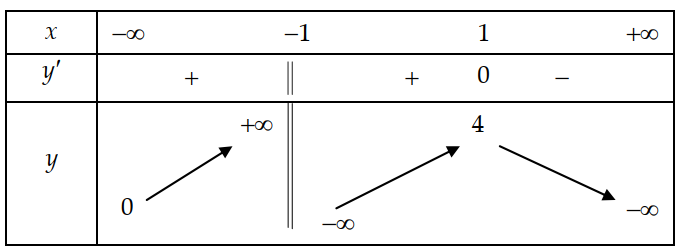
Khảng định nào sau đây là đúng?
-
Câu 44:
Cho hàm số y=f(x) xác định, liên tục trên \(\mathbb{R}\) và có bảng biến thiên sau
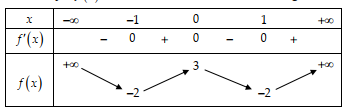
Khẳng định nào sau đây đúng?
-
Câu 45:
Cho hàm số y = f (x) xác định, liên tục trên \(\mathbb{R}\) và có bảng biến thiên sau:
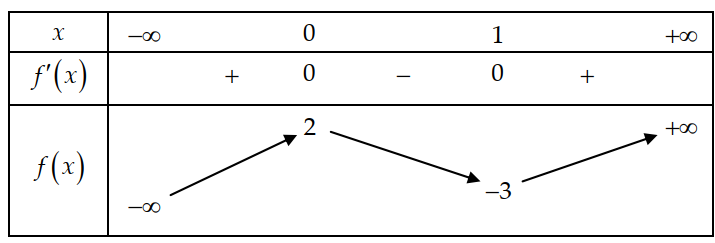
Khẳng định nào sau đây đúng?
-
Câu 46:
Cho hàm số y = f (x) xác định, liên tục trên \(\mathbb{R}\)và có bảng biến thiên sau
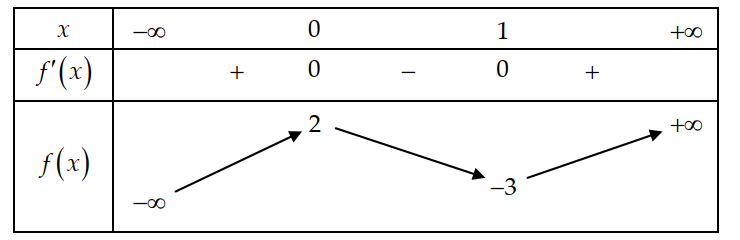
Khẳng định nào sau đây sai?
-
Câu 47:
Tìm tập hợp tất cả các giá trị thực của m để đồ thị hàm số y = x³ - 3mx² + 3m³ có có hai điểm cực trị A và B sao cho tam giác OAB có diện tích bằng 48 (với O là gốc tọa độ)
-
Câu 48:
Tìm tập hợp tất cả các giá trị thực của m để đồ thị hàm số y = x⁴ - 2(m + 1)x² + m² có ba điểm cực trị tạo thành một tam giác vuông.
-
Câu 49:
Tìm tập hợp tất cả các giá trị thực của tham số m để hàm số y = mx⁴ + (m² - 9)x² + 10 có ba điểm cực trị.
-
Câu 50:
Tìm tập hợp tất cả giá trị thực của tham số m để đồ thị hàm số y = x⁴ - 2(m + 1) x² + m có ba điểm cực trị A, B, C sao cho OA = BC;trong đó O là gốc tọa độ, A là điểm cực trị thuộc trục tung, B và C là hai điểm cực trị còn lại.











