Trắc nghiệm Đường tiệm cận Toán Lớp 12

Câu 1:

Đồ thị hàm số nào sau đây không có tiệm cận đứng? 

Câu 2:

Đường tiệm cận ngang của đồ thị hàm số \(y=\frac{1}{x-2} \text { là }\)

Câu 3:

Đường tiệm cận ngang của đồ thị hàm số \(y=\frac{2 x+7}{x-1}\) là:

Câu 4:

Đường tiệm cận đứng của đồ thị hàm số \(y=\frac{x+1}{x-2} 1 \) là:

Câu 5:

Đường tiệm cận đứng của đồ thị hàm số \(y=\frac{2 x+1}{x-1}\) là:

Câu 6:

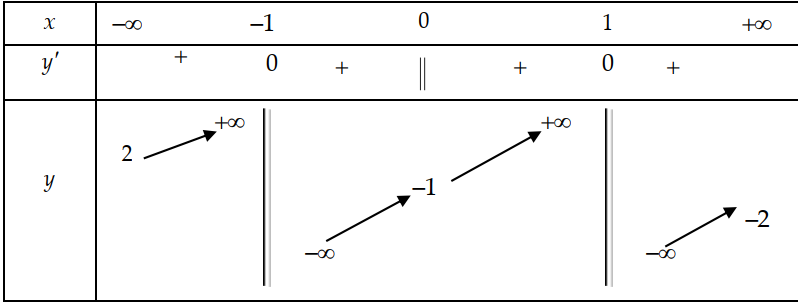
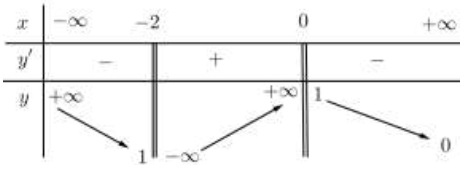
Cho hàm số (x) có bảng biến thiên như hình bên dưới:

Tìm số tiệm cận của đồ thị hàm số đã cho.

Câu 7:

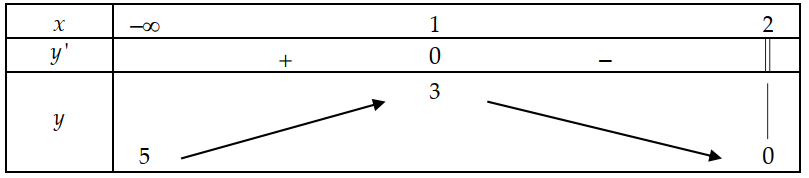
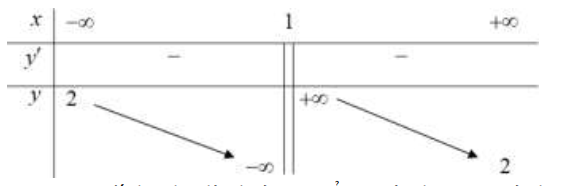
Trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hàm số nào có bảng biến thiên sau? 

Câu 8:

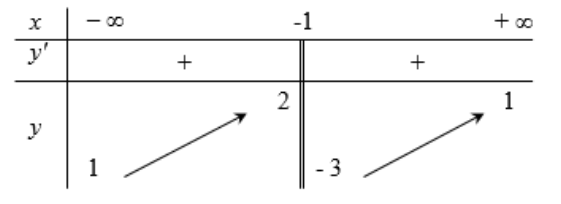
Trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hàm số nào có bảng biến thiên sau?

Câu 9:

Cho hàm số \(y=f(x)\) có bảng biến thiên sauKhẳng định nào sau đây đúng 

Câu 10:

Cho hàm số y =f(x) xác định trên \((-\infty ; 2) \) và có bảng biến thiên sau: 

Khẳng định nào sau đây đúng?

Câu 11:

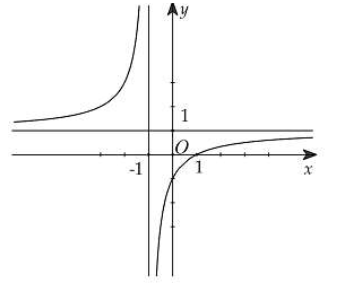
Đồ thị như hình vẽ là của một trong bốn hàm số được cho ở các phương án A, B, C, D. Hỏi đó là hàm số nào? 

Câu 12:

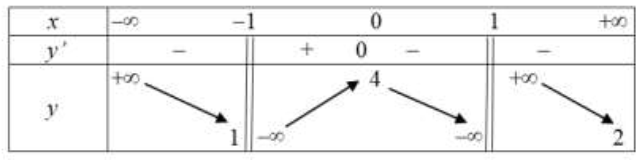
Cho hàm số y=f(x) xác định trên \(\mathbb{R} \backslash\{1\},\), liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình dưới đây. Hỏi đồ thị hàm số đã cho có bao nhiêu đường tiệm cận 

Câu 13:

Cho hàm số \(y=f(x)\) có bảng biến thiên như hình vẽ dưới đây. Hỏi đồ thị của hàm số đã cho có bao nhiêu đường tiệm cận? 

Câu 14:

Cho hàm số y \(y=f(x) \text { có }\) có bảng biến thiên như hình vẽ dưới đây: 

Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là:

Câu 15:

Cho hàm số \(y=f(x)\) có bảng biến thiên như sau: 

Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho bằng

Câu 16:

Cho hàm số \(y=f(x)\) có bảng biến thiên như sau: 

Tiệm cận đứng của đồ thị hàm số đã cho là đường thẳng có phương trình

Câu 17:

Cho hàm số \(y=f(x)\) có bảng biến thiên như sau: 

Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y =f(x) là:

Câu 18:

\(\text { Cho hàm số } y=f(x) \text { có } \lim _{x \rightarrow-\infty} f(x)=2, \lim _{x \rightarrow+\infty} f(x)=-\infty \text { . }\)Khẳng định nào sau đây đúng?

Câu 19:

Cho hàm số f(x) xác định trên \(\mathbb{R} \backslash\{1\}\) và có \(\lim\limits _{x \rightarrow-\infty} f(x)=-2, \lim\limits _{x \rightarrow 1^{+}} f(x)=+\infty \text { , }\lim \limits_{x \rightarrow 1^{-}} f(x)=+\infty, \lim\limits _{x \rightarrow+\infty} f(x)=2 .\) Khẳng định nào sau đây đúng? 

Câu 20:

Nếu hàm số y=f(x) thỏa mãn điều kiện \(\lim \limits_{x \rightarrow-\infty} f(x)=2021\) thì đồ thị hàm số có đường tiệm cận ngang là 

Câu 21:

Đồ thị hàm số nào sau đây có hai tiệm cận tạo với hai trục tọa độ một tứ giác có diện tích bằng 12?

Câu 22:

Cho hàm số \(y = \dfrac{{3x - 1}}{{x + 4}}\). Gọi \(I\) là giao điểm của hai đường tiệm cận. Tính \(OI\).

Câu 23:

Tiệm cận ngang của đồ thị hàm số \(y = \dfrac{{{x^2} - 12x + 27}}{{{x^2} - 4x + 5}}\) là:

Câu 24:

Tiệm cận ngang của đồ thị hàm số \(y =  - \dfrac{3}{{x - 2}}\) là:

Câu 25:

Tiệm cận đứng của đồ thị hàm số \(y =  - \dfrac{3}{{x - 2}}\) là:

Câu 26:

Tiệm cận đứng của đồ thị hàm số \(y = \dfrac{{2{x^2} - x + 2}}{{{x^2} - 5}}\) là:

Câu 27:

Đường tiệm cận đứng của đồ thị hàm số \(y = \dfrac{{3x + 1}}{{3 - 2x}}\) là:

Câu 28:

Đường tiệm cận ngang của đồ thị hàm số \(y = \dfrac{{3x + 1}}{{3 - 2x}}\) là:

Câu 29:

Số tiệm cận của đồ thị hàm số \(y = \dfrac{{3x + 1}}{{3 - 2x}}\) là:

Câu 30:

Đồ thị hàm số \(y = \dfrac{{5x - 1 - \sqrt {{x^2} - 2} }}{{x - 4}}\) có đường tiệm cận đứng là:

Câu 31:

Đồ thị hàm số \(y = \dfrac{{5x - 1 - \sqrt {{x^2} - 2} }}{{x - 4}}\) có bao nhiêu đường tiệm cận ngang?

Câu 32:

Đồ thị hàm số \(y = \dfrac{{3x + \sqrt {{x^2} + 1} }}{{2 + \sqrt {3{x^2} + 2} }}\) có bao nhiêu đường tiệm cận ngang?

Câu 33:

Đường tiệm cận ngang của đồ thị hàm số \(y = \dfrac{{{x^2} + 3x}}{{{x^2} - 4}}\) là:

Câu 34:

Đồ thị hàm số \(y = \dfrac{{{x^2} + 3x}}{{{x^2} - 4}}\) có bao nhiêu đường tiệm cận đứng?

Câu 35:

Đường tiệm cận đứng của đồ thị hàm số \(y = \dfrac{{{x^2} - x - 2}}{{{{(x - 1)}^2}}}\) là:

Câu 36:

Đồ thị hàm số \(y = \dfrac{{{x^2} - x - 2}}{{{{(x - 1)}^2}}}\) có đường tiệm cận ngang là:

Câu 37:

Đồ thị hàm số \(y = \dfrac{{ - 4}}{{x + 1}}\) có đường tiệm cận đứng là:

Câu 38:

Đồ thị hàm số \(y = \dfrac{{ - 4}}{{x + 1}}\) có đường tiệm cận ngang là:

Câu 39:

Đồ thị hàm số \(y = \dfrac{5}{{2 - 3x}}\) có đường tiệm cận ngang là:

Câu 40:

Đồ thị hàm số \(y = \dfrac{5}{{2 - 3x}}\) có đường tiệm cận đứng là:

Câu 41:

Đường tiệm cận đứng của đồ thị hàm số \(y = \dfrac{{3 - 2x}}{{3x + 1}}\) là:

Câu 42:

Đường tiệm cận ngang của đồ thị hàm số \(y = \dfrac{{3 - 2x}}{{3x + 1}}\) là:

Câu 43:

Đồ thị hàm số \(y = \dfrac{{2x - 1}}{{x + 2}}\) có đường tiệm cận ngang là đường thẳng nào sau đây?

Câu 44:

Đồ thị hàm số \(y = \dfrac{{2x - 1}}{{x + 2}}\) có đường tiệm cận đứng là đường thẳng nào sau đây?

Câu 45:

Đường thẳng y=2 là tiệm cận ngang của đồ thị hàm số nào dưới đây?

Câu 46:

Đồ thị hàm số \(y=\frac{\left(m^{2}+m\right) x-1}{x-2}\) có đường tiệm cận ngang qua điểm \(A(-3 ; 2)\) khi:

Câu 47:

Đồ thị hàm số \(y=\frac{2 x+1}{x-3}\) có tiệm cận đứng là đường thẳng nào sau đây ? 

Câu 48:

Đồ thị hàm số nào sau đây nhận đường thẳng x=2 làm đường tiệm cận:

Câu 49:

Cho hàm số y=f(x) có bảng biến thiên:

Đồ thị hàm số có tiệm cận đứng là đường thẳng có phương trình là

Câu 50:

Đồ thị hàm số \(y=\frac{\sqrt{x^{2}-4}}{x^{2}-5 x+6}\) có tất cả bao nhiêu tiệm cận đứng và tiệm cận ngang?