Trắc nghiệm Hàm số lũy thừa Toán Lớp 12
-
Câu 1:
Tập nghiệm của bất phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac+ % gacaGGNbWaaSbaaSqaaiaaiodaaeqaaOWaaSaaaeaacaaI0aGaamiE % aiabgUcaRiaaiAdaaeaacaWG4baaaiabgsMiJkaaicdaaaa!408F! {\log _3}\frac{{4x + 6}}{x} \le 0\) là:
-
Câu 2:
Tập nghiệm của bất phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac+ % gacaGGNbWaaSbaaSqaamaalaaabaGaaGymaaqaaiaaikdaaaaabeaa % kmaabmaabaGaamiEaiabgkHiTiaaigdaaiaawIcacaGLPaaacqGHLj % YScaaIWaaaaa!412E! {\log _{\frac{1}{2}}}\left( {x - 1} \right) \ge 0\) là:
-
Câu 3:
Tìm tập nghiệm của bất phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac+ % gacaGGNbWaaSbaaSqaamaalaaabaGaaGymaaqaaiaaikdaaaaabeaa % kmaabmaabaGaamiEamaaCaaaleqabaGaaGOmaaaakiabgkHiTiaaio % dacaWG4bGaey4kaSIaaGOmaaGaayjkaiaawMcaaiabgwMiZkabgkHi % Tiaaigdaaaa!45AC! {\log _{\frac{1}{2}}}\left( {{x^2} - 3x + 2} \right) \ge - 1\)
-
Câu 4:
Tìm tập nghiệm S của bất phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac+ % gacaGGNbWaaSbaaSqaamaalaaabaGaaGymaaqaaiaaikdaaaaabeaa % kmaalaaabaGaaGOmaaqaaiaadIhacqGHsislcaaIXaaaaiabg6da+i % aaikdaaaa!3FB6! {\log _{\frac{1}{2}}}\frac{2}{{x - 1}} > 2\)
-
Câu 5:
Tập nghiệm của bất phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac+ % gacaGGNbWaaSbaaSqaamaalaaabaGaaGymaaqaaiaaikdaaaaabeaa % kiaadIhadaahaaWcbeqaaiaaikdaaaGccqGHLjYScqGHsislcaaIXa % aaaa!3FDF! {\log _{\frac{1}{2}}}{x^2} \ge - 1\) là
-
Câu 6:
Tìm tập nghiệm của bất phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac+ % gacaGGNbWaaSbaaSqaaiaaicdacaGGSaGaaGynaaqabaGcdaqadeqa % aiaaikdacaWG4bGaeyOeI0IaaGymaaGaayjkaiaawMcaaiabg6da+i % abgkHiTiaaikdaaaa!42BF! {\log _{0,5}}\left( {2x - 1} \right) > - 2\)
-
Câu 7:
Tập nghiệm của bất phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaG4maiabgY % da8iGacYgacaGGVbGaai4zamaaBaaaleaacaaIYaaabeaakiaadIha % cqGH8aapcaaI0aaaaa!3E35! 3 < {\log _2}x < 4\) là:
-
Câu 8:
Giải bất phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac+ % gacaGGNbWaaSbaaSqaamaalaaabaGaaG4maaqaaiaaisdaaaaabeaa % kmaabmaabaaeaaaaaaaaa8qacaaIYaGaamiEaiabgkHiTiaaigdaa8 % aacaGLOaGaayzkaaWdbiabg6da+iaaikdaaaa!4171! {\log _{\frac{3}{4}}}\left( {2x - 1} \right) > 2\) ta được:
-
Câu 9:
Tập nghiệm của bất phương trình \({\log _{\frac{1}{2}}}\left( {2x - 1} \right) > - 1\) là:
-
Câu 10:
Bất phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac+ % gacaGGNbWaaSbaaSqaaiaaikdaaeqaaOWaaeWaaeaacaWG4bWaaWba % aSqabeaacaaIYaaaaOGaeyOeI0IaaGOmaiaadIhacqGHRaWkcaaIZa % aacaGLOaGaayzkaaGaeyOpa4JaaGymaaaa!4337! {\log _2}\left( {{x^2} - 2x + 3} \right) > 1\) có tập nghiệm là
-
Câu 11:
Tìm tọa độ giao điểm M của hai đồ thị hàm số \(y = 3^x\) và \(y = \frac{1}{3}\).
-
Câu 12:
Đường cong ở hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn
phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?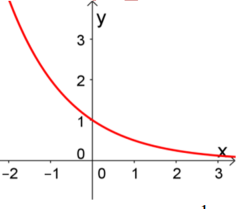
-
Câu 13:
Đường cong trong hình bên dưới là đồ thị của một hàm số trong bốn hàm số được liệt kê ở
bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?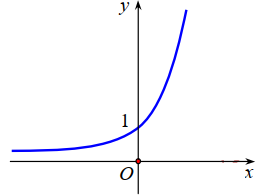
-
Câu 14:
Hàm số nào trong các hàm số dưới đây có đồ thị phù hợp với hình vẽ bên?
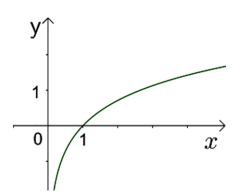
-
Câu 15:
Cho \( \alpha, \beta \) là các số thực. Đồ thị các hàm số \(y = x^{\alpha} , y = x^{\beta}\)trên khoảng \((0; +\infty)\) được cho trong hình vẽ bên. Khẳng định nào sau đây là đúng?
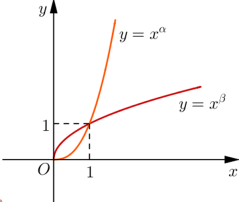
-
Câu 16:
Cho hàm số \(y=x^{-\sqrt2}\) . Mệnh đề nào sau đây là sai?
-
Câu 17:
Cho hàm số \(y = x^{e-3}\)trong các kết luận sau kết luận nào sai?
-
Câu 18:
Cho hàm số \(y = x^ {-\sqrt{2017}}\) . Mệnh đề nào dưới đây là đúng về đường tiệm cận của đồ thị hàm số
-
Câu 19:
Hình vẽ bên là đồ thị các hàm số \(y = x^a , y = x^b , y = x^c\) trên miền \((0;+\infty)\) . Hỏi trong các số a, b, c số nào nhận giá trị trong khoảng (0; 1) ?
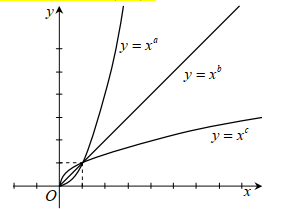
-
Câu 20:
Hàm số nào trong hàm số sau đây có đồ thị phù hợp với hình vẽ bên
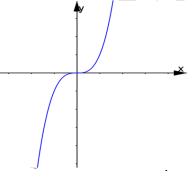
-
Câu 21:
Tính đạo hàm của hàm số \(y = log (ln 2x)\)
-
Câu 22:
Cho hàm số \(f (x) = ln (x⁴ +1)\) . Đạo hàm f'(1) bằng
-
Câu 23:
Đạo hàm của hàm số \(y = log_3( x + 1) - 2 ln ( x -1) + 2x\) tại điểm x = 2 bằng
-
Câu 24:
Cho hàm số \(y = 2xe^x + 3sin 2x\) .Khi đó y'(0) có giá trị bằng
-
Câu 25:
Đạo hàm của hàm số \(y = log (2 sin x -1)\) trên tập xác định là:
-
Câu 26:
Đạo hàm của hàm số \(y = log_8 (x² - 3x - 4)\) là
-
Câu 27:
Cho hàm số \(f ( x) = ln (4x - x² )\). Chọn khẳng định đúng?
-
Câu 28:
Tính đạo hàm của hàm số \(y = log_{2017}(x +1)\)
-
Câu 29:
Đạo hàm của hàm số \(y = log_3(4x + 1)\) là
-
Câu 30:
Tính đạo hàm của hàm số \(y = \sqrt {x\sqrt[3]{{x\sqrt[4]{x}}}} \)
-
Câu 31:
Cho hàm số \(y=x^{\pi}\) . Tính y''(1).
-
Câu 32:
Đạo hàm của hàm số \(y = {\left( {5{x^2} - x + 2} \right)^{\frac{1}{3}}}\)
-
Câu 33:
Hàm số \(y=log_{a^2-2a+1}x\) nghịch biến trong khoảng \((0;+\infty)\) khi
-
Câu 34:
Hàm số \(y = log_2 (x^3 - 4x)\) có bao nhiêu điểm cực trị?
-
Câu 35:
Hàm số \( y = log_{0,5}(-x² + 2x)\) đồng biến trên khoảng nào sau đây?
-
Câu 36:
Hàm số \(y = \ln \left( {x + 2} \right) + \frac{3}{{x + 2}}\) đồng biến trên khoảng nào ?
-
Câu 37:
Đồ thị hàm số \(y=\frac{lnx}{x}\)có tọa độ điểm cực đại là \((a;b)\). Khi đó ab bằng
-
Câu 38:
Hàm số \(log_2(x^3-4x)\) có bao nhiêu điểm cực trị?
-
Câu 39:
Trong các hàm số sau, hàm số nào nghịch biến trong khoảng \((0;+\infty)\)
-
Câu 40:
Hàm số nào dưới đây đồng biến trên \(\mathbb{R}\)
-
Câu 41:
Trong các hàm số sau, hàm số nào nghịch biến trên khoảng \((0;+\infty)\)
-
Câu 42:
Trong các hàm số sau, hàm số nào đồng biến trên \(\mathbb{R}\)
-
Câu 43:
Cho hàm số \(y=\frac{1}{4^x}\) Mệnh đề nào sau đây là mệnh đề SAI?
-
Câu 44:
Hàm số nào dưới đây đồng biến trên tập xác định của nó?
-
Câu 45:
Cho hàm số \(y = {\left( {\frac{3}{4}} \right)^{{x^2} - 2x + 2}}\) . Trong các khẳng định dưới đây, khẳng định nào đúng?
-
Câu 46:
Hàm số nào sau đây nghịch biến trên tập xác định của nó?
-
Câu 47:
Hàm số nào sau đây đồng biến trên tập xác định của nó?
-
Câu 48:
Đồ thị hàm số nào sau đây đối xứng với đồ thị hàm số \(y = 10^{-x}\)qua đường thẳng y = x .
-
Câu 49:
Cho hàm số \( y = log_2 x\) . Mệnh đề nào dưới đây sai?
-
Câu 50:
Cho hàm số \(y = log_{\sqrt3}x\) . Mệnh đề nào dưới đây là mệnh đề sai?











