Trắc nghiệm Khảo sát sự biến thiên và vẽ đồ thị của hàm số Toán Lớp 12
-
Câu 1:
Số giao điểm của đồ thị hàm số \(y = 2{x^4} – 3{x^2}\) với trục hoành là
-
Câu 2:
Đồ thị hàm số \(y = {x^4} – {x^2} + 1\) cắt trục tung tại điểm có tung độ bằng
-
Câu 3:
Đồ thị hàm số \(y = {x^2} – \left| x \right| + 1\) cắt trục tung tại điểm có tung độ bằng
-
Câu 4:
Đồ thị hàm số \(y = \sqrt {{{\sin }^2}x + 4} \) cắt trục tung tại điểm có tung độ bằng
-
Câu 5:
Đồ thị hàm số \(y = \sqrt {{x^2} + 4} \) cắt trục tung tại điểm có tung độ bằng
-
Câu 6:
Đồ thị hàm số \(y = {\log _2}\left( {{x^2} + 2} \right)\) cắt trục tung tại điểm có tung độ bằng
-
Câu 7:
Đồ thị hàm số \(y = \cos x\) cắt trục tung tại điểm có tung độ bằng
-
Câu 8:
Đồ thị hàm số \(y = {e^{2x}}\) cắt trục tung tại điểm có tung độ bằng
-
Câu 9:
Đồ thị hàm số \(y = \frac{{2x + 3}}{{x + 3}}\) cắt trục tung tại điểm có tung độ bằng
-
Câu 10:
Đồ thị hàm số \(y = \frac{{{x^2} – x – 1}}{{x + 1}}\) cắt trục tung tại điểm có tung độ bằng
-
Câu 11:
Đồ thị hàm số \(y = {x^4} – 3{x^2} – 1\) cắt trục tung tại điểm có tung độ bằng
-
Câu 12:
Đồ thị của hàm số \(y = {x^3} – 3x + 2\) cắt trục tung tại điểm có tung độ bằng
-
Câu 13:
Giao điểm của đồ thị hàm số \(y = \dfrac{{2x + 1}}{{2x - 1}}\) với đường thẳng y = x + 2 là:
-
Câu 14:
Phương trình tiếp tuyến của đồ thị hàm số \(y = {x^4} - 2{x^2} - 3\) song song với đường thẳng y = 24x - 1 là:
-
Câu 15:
Phương trình tiếp tuyến của đồ thị hàm số \(y = {x^4}-2{x^2}\) tại điểm có hoành độ x = - 2 là:
-
Câu 16:
Xác định giá trị của tham số \(m\) để hàm số \(y = {x^3} - 3\left( {m - 1} \right){x^2} - 3\left( {m + 1} \right)x - 5\) có cực trị.
-
Câu 17:
Biểu thức tổng quát của hàm số có đồ thị như hình dưới đây là:
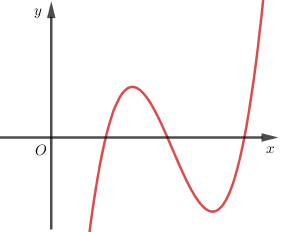
-
Câu 18:
Hàm số \(y = {x^4} + \left( {{m^2} - 4} \right){x^2} + 5\) có ba cực trị khi:
-
Câu 19:
Hàm số \(y = {x^3} + \left( {m + 3} \right){x^2} + mx - 2\) đạt cực tiểu tại x = 1 khi:
-
Câu 20:
Cho hàm số: \(y = {x^3} - (m + 4){x^2} - 4x + m\) (1). Có bao nhiêu điểm mà đồ thị của hàm số (1) đi qua với mọi giá trị của m?
-
Câu 21:
Tìm giá trị của tham số m để hàm số \(y = (m - 1){x^4} - m{x^2} + 3\) có đúng một cực trị.
-
Câu 22:
Tìm giá trị của tham số m để hàm số\(y = - \dfrac{1}{3}({m^2} + 6m){x^3} - 2m{x^2} + 3x + 1\) đạt cực đại tại x = - 1.
-
Câu 23:
Tìm giá trị của tham số m để hàm số \(y = {x^3} + (m + 3){x^2} + mx - 2\) đạt cực tiểu tại x = 1.
-
Câu 24:
Cho phương trình \(x^{3}-3 x^{2}+1-m=0(1)\) Điều kiện của tham số m để (1)có ba nghiệm phân biệt thỏa\(x_{1}<1<x_{2}<x_{3}\) khi
-
Câu 25:
Cho hàm số \(y=-2 x^{3}+3 x^{2}-1\) có đồ thị (C) như hình vẽ. Dùng đồ thị (C) suy ra tất cả giá trị tham số m để phương trình \(2 x^{3}-3 x^{2}+2 m=0\) có ba nghiệm phân biệt là
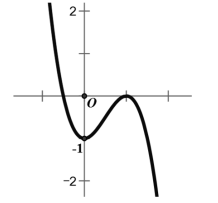
-
Câu 26:
Tất cả giá trị của thm số m để phương trình \(x^{3}-3 x-m+1=0\) có ba nghiệm phân biệt, trong đó có hai nghiệm dương là
-
Câu 27:
Tất cả giá trị của tham số m để đồ thị hàm số \((C): y=-2 x^{3}+3 x^{2}+2 m-1\) cắt trục hoành tại ba điểm phân biệt là
-
Câu 28:
Tất cả giá trị của tham số m để đồ thị hàm số \(y=-2 x^{4}+2 x^{2}+1\) cắt đường thẳng y =3m tại ba điểm phân biệt là
-
Câu 29:
Tất cả giá trị của tham số m để phương trình \(x^{4}-2 x^{2}-m+3=0\) có hai nghiệm phân biệt là
-
Câu 30:
Tất cả giá trị của tham số m để phương trình \(x^{4}-2 x^{2}-m+3=0\) có bốn nghiệm phân biệt là
-
Câu 31:
Cho hàm số \(y=(x-2)\left(x^{2}+m x+m^{2}-3\right)\). Tất cả giá trị của thma số m để đồ thị hàm số đã cho cắt trục hoành tại ba điểm phân biệt là
-
Câu 32:
Cho hàm số \(y=-x^{4}+2 x^{2}+m\) . Tất cả giá trị của tham số m để đồ thị hàm số đã cho cắt trục hoành tại ít nhất ba điểm phân biệt là
-
Câu 33:
Tất cả các giá trị của tham số m để phương trình \(x^{4}-3 x^{2}+m=0\) có bốn nghiệm phân biệt là
-
Câu 34:
Cho hàm số \(y=x^{4}-4 x^{2}-2\) có đồ thị (C) và đường thẳng \(d: y=m\) . Tất cả các giá trị của tham số m để d cắt (C) tại bốn điểm phân biệt là
-
Câu 35:
Tất cả giá trị của tham số m để đồ thị \((C): y=x^{4}-2 x^{2}-3\) cắt đường thẳng d: y=m tại bốn điểm phân biệt là
-
Câu 36:
Tất cả giá trị của tham số m để đồ thị \((C): y=x^{3}-3 x^{2}+2\) cắt đường thẳng \(d: y=m\) tại ba điểm phân biệt là
-
Câu 37:
Tất cả giá trị của tham số m để phương trình \(x^{3}-3 x-m+1=0\) có ba nghiệm phân biệt là
-
Câu 38:
Với tất cả giá trị nào của tham số m thì phương trình \(x^{4}-2 x^{2}=m+3\) có bốn nghiệm phân biệt?
-
Câu 39:
Đường thẳng y=m không cắt đồ thị hàm số \(y=-2 x^{4}+4 x^{2}+2\) thì tất cả các giá trị tham số m là
-
Câu 40:
Đồ thị hàm số \(y=x^{3}-3 x^{2}+1\) cắt đường thẳng y = m tại ba điểm phân biệt thì tất cả các giá trị tham số m thỏa mãn là
-
Câu 41:
Tiệm cận ngang của đồ thị hàm số \((H): y=\frac{x+2}{x+1}\) cắt đồ thị hàm số \((C): y=2 x^{4}-x^{2}\) tại các điểm có tọa độ là
-
Câu 42:
Tọa độ trung điểm I của đoạn thẳng MN với M, N là giao điểm của đường thẳng \($d: y=x+1$ và\) và đồ thị hàm số \(\text { (C) }: y=\frac{2 x+2}{x-1}\) là
-
Câu 43:
ho hàm số \(y=x^{4}-4 x^{2}-2\) có đồ thị (C) và đồ thị \((P): y=1-x^{2}\). Số giao điểm của (P) và đồ thị (C) là
-
Câu 44:
Giao điểm giữa đồ thị \(\text { (C) }: y=\frac{x^{2}-2 x-3}{x-1}\) và đường thẳng \((d): y=x+1\) là
-
Câu 45:
Số giao điểm của đồ thị hàm số \(y=\frac{x^{2}-4 x+3}{x+2}\)và trục hoành là
-
Câu 46:
Cho hàm số \(y=2 x^{3}-3 x^{2}+1\) có đồ thị ( C)và đường thẳng \(d: y=x-1\). Số giao điểm của ( C) và d là
-
Câu 47:
Đường thẳng\((C): y=\frac{2 x-1}{x+1}\) cắt đồ thị hàm số \(d: y=2 x-3\) tại các điểm có tọa độ là
-
Câu 48:
Số giao điểm của đồ thị hàm số \(y=(x+3)\left(x^{2}+3 x+2\right)\) với trục Ox là
-
Câu 49:
Số giao điểm của đồ thị hàm số \(y=-x^{4}+2 x^{2}-1\) với trục Ox là
-
Câu 50:
Hàm số \(y=\frac{2+2 x}{2+x}\) có đồ thị là hình vẽ nào sau đây?











