Trắc nghiệm Khảo sát sự biến thiên và vẽ đồ thị của hàm số Toán Lớp 12
-
Câu 1:
Cho hàm số y = ax4 + bx2 + c có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng?
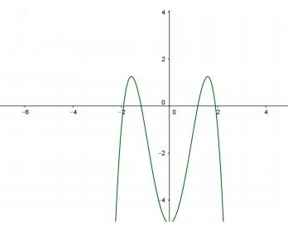
-
Câu 2:
Cho các phát biểu sau:
I. Đồ thị hàm số có y = x4 – x + 2 có trục đối xứng là Oy.
II. Hàm số f(x) liên tục và có đạo hàm trên khoảng (a;b) đạt cực trị tại điểm x0 thuộc khoảng (a;b) thì tiếp tuyến tại điểm M(x0,f(x0)) song song với trục hoành.
III. Nếu f(x) nghịch biến trên khoảng (a;b) thì hàm số không có cực trị trên khoảng (a;b).
IV. Hàm số f(x) xác định và liên tục trên khoảng (a;b) và đạt cực tiểu tại điểm x0 thuộc khoảng (a;b) thì f(x) nghịch biến trên khoảng (a;x0) và đồng biến trên khoảng (x0;b).
Các phát biểu đúng là:
-
Câu 3:
Tiếp tuyến tại điểm cực tiểu của đồ thị hàm số \(y = \frac{1}{3}{x^3} - 2{x^2} + 3x - 5\) là đường thẳng
-
Câu 4:
Giá trị của m để phương trình \(x+\sqrt{2 x^{2}+1}=m\) có nghiệm là:
-
Câu 5:
Tìm tất cả các giá trị thực của tham số m để phương trình \(m \sqrt{2+\tan ^{2} x}=m+\tan x\) có ít nhất một nghiệm thực.
-
Câu 6:
Tìm tất cả giá trị của m để phương trình \(\sqrt[4]{x^{2}+1}-\sqrt{x}=m\) có nghiệm
-
Câu 7:
Với mọi m ∈ (-1; 1) phương trình \({\sin ^2}x + \cos x = m\) có mấy nghiệm trên đoạn [0; π] ?
-
Câu 8:
Với m > 0 phương trình \(\left| x \right| = \sqrt[3]{{2{x^2} - \left| x \right| + m - 1}}\) có ít nhất mấy nghiệm?
-
Câu 9:
Với giá trị nào của tham số m thì phương trình \(x+\sqrt{4-x^{2}}=m\) có nghiệm?
-
Câu 10:
Tìm m để phương trình \({x^4} - 2{x^2} + 3--{m^2} + 2m = 0\) có đúng ba nghiệm phân biệt
-
Câu 11:
Cho hàm số \(y = 3x - 4{x^3}\). Có nhiều nhất mấy tiếp tuyến với đồ thị hàm số đi qua điểm M(1; 3) ?
-
Câu 12:
Tiếp tuyến của parabol \(y = 4 - {x^2}\) tại điểm (1; 3) tạo với hai trục tọa độ một tam giác vuông. Diện tích tam giác vuông đó là
-
Câu 13:
Tìm tập hợp tất cả các giá trị của tham số m sao cho bất phương trình sau có nghiệm:\(\sqrt{x+5}+\sqrt{4-x} \geq m\)
-
Câu 14:
Đường thẳng y = 3x + m là tiếp tuyến của đường cong \(y = {x^3} + 2\) khi m bằng
-
Câu 15:
Đồ thị hàm số \(y = {x^3} - 3x\) cắt
-
Câu 16:
Cho đồ thị hàm số f(x) như hình bên. Hàm số nào dưới đây tương ứng với đồ thị đó?
-
Câu 17:
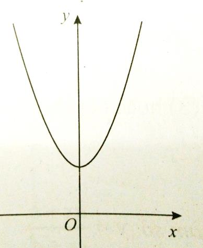
Cho hàm số \(y = {x^4} + \left( {{m^2} + 1} \right){x^2} + 1\). Hình nào dưới đây mô tả chính xác nhất đồ thị hàm số trên?
-
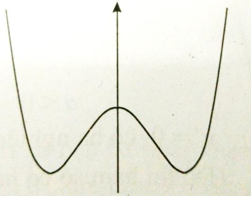
Câu 18:
Cho hàm số \(y=2{x^3} - 3\left( {m + 1} \right){x^2} + 6\left( {m + 1} \right)2x + 1\). Hình nào dưới đây mô tả chính xác nhất đồ thị hàm số trên?
-
Câu 19:
Tìm m để phương trình \({x^3} + 3{x^2} = m\) có ba nghiệm phân biệt
-
Câu 20:
Gọi M, N là giao điểm của y = x+1 và \(y\; = \frac{{\;2x + 4\;}}{{x - 1}}\) Khi đó hoành độ trung điểm của I của đoạn thẳng MN bằng
-
Câu 21:
Cho hàm số \(y = \frac{1}{3}{x^3} - 2{x^2} + 3x + 1\). Tìm phương trình tiếp tuyến của đồ thị (C), biết tiếp tuyến đó song song với đường thẳng y = 3x −1
-
Câu 22:
Cho hàm số \(y = \frac{1}{3}{x^3} + {x^2} - 2\)
Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ là nghiệm của phương trình y'' = 0 là
-
Câu 23:
Tìm m để bất phương trình \({x^4} + 2{x^2} \ge m\) luôn đúng.
-
Câu 24:
Trong các mệnh đề sau, mệnh đề nào đúng?
A. I(1; 0) là tâm đối xứng của y=x+1x−1y=x+1x-1
B. I(1; 0) là tâm đối xứng của y=−x3+3x2−2y=-x3+3x2-2
C. I(1; 0) là điểm thuộc đồ thị y=x+1x−1y=x+1x-1
D. I(1; 0) là giao điểm của y=x3−3x2−2y=x3-3x2-2 với trục hoành.
-
Câu 25:
Tâm đối xứng của đồ thị hàm số \(y = - {x^3} - 3{x^2} + 1\) là:
-
Câu 26:
Đồ thị trong hình dưới đây là đồ thị của đồ thị hàm số nào?
-
Câu 27:
Đường cong trong hình dưới đây là đồ thị của một hàm số trong 4 hàm số được liệt kê ở 4 phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
-
Câu 28:
Gọi (H) là đồ thị hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9maalaaabaGaaGOmaiaadIhacqGHRaWkcaaIZaaabaGaamiEaiab % gUcaRiaaigdaaaaaaa!3DF9! y = \frac{{2x + 3}}{{x + 1}}\). Điểm \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamytaiaacI % cacaWG4bWaaSbaaSqaaiaaicdaaeqaaOGaai4oaiaadMhadaWgaaWc % baGaaGimaaqabaGccaGGPaaaaa!3CB9! M({x_0};{y_0})\) thuộc (H) có tổng khoảng cách đến hai đường tiệm cận là nhỏ nhất, với \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEamaaBa % aaleaacaaIWaaabeaakiabgYda8iaaicdaaaa!399F! {x_0} < 0\) khi đó \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEamaaBa % aaleaacaaIWaaabeaakiabgUcaRiaadMhadaWgaaWcbaGaaGimaaqa % baaaaa!3AA7! {x_0} + {y_0}\) bằng?
-
Câu 29:
Cho đồ thị \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaaca % WGdbaacaGLOaGaayzkaaGaaiOoaiaaykW7caaMc8UaamyEaiabg2da % 9maalaaabaGaamiEaiabgkHiTiaaiodaaeaacaWG4bGaey4kaSIaaG % ymaaaaaaa!436D! \left( C \right):\,\,y = \frac{{x - 3}}{{x + 1}}\). Biết rằng, có hai điểm phân biệt thuộc đồ thị (C) và cách đều hai trục toạ độ. Giả sử các điểm đó lần lượt là M và N. Tìm độ dài của đoạn thẳng MN.
-
Câu 30:
Gọi M(a;b) là điểm thuộc đồ thị hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9maalaaabaGaaGOmaiaadIhacqGHRaWkcaaIXaaabaGaamiEaiab % gUcaRiaaikdaaaaaaa!3DF9! y = \frac{{2x + 1}}{{x + 2}}\) và có khoảng cách từ M đến đường thẳng \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamizaiaacQ % dacaWG5bGaeyypa0JaaG4maiaadIhacqGHRaWkcaaI2aaaaa!3CFB! d:y = 3x + 6\) nhỏ nhất. Tìm giá trị của biểu thức \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamivaiabg2 % da9iaaiodacaWGHbWaaWbaaSqabeaacaaIYaaaaOGaey4kaSIaamOy % amaaCaaaleqabaGaaGOmaaaaaaa!3D1B! T = 3{a^2} + {b^2}\).
-
Câu 31:
Tìm trên mỗi nhánh của đồ thị (C): \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVCI8FfYJH8YrFfeuY-Hhbbf9v8qqaqFr0xc9pk0xbb % a9q8WqFfeaY-biLkVcLq-JHqpepeea0-as0Fb9pgeaYRXxe9vr0-vr % 0-vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadMhacqGH9a % qpdaWcaaqaaiaaisdacaWG4bGaeyOeI0IaaGyoaaqaaiaadIhacqGH % sislcaaIZaaaaaaa!3E0F! y = \frac{{4x - 9}}{{x - 3}}\) các điểm \(M_1;M_2\) để độ dài \(M_1M_2\) đạt giá trị nhỏ nhất, giá trị nhỏ nhất đó bằng:
-
Câu 32:
Tính tổng các hoành độ của những điểm thuộc đồ thị \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaaca % WGdbaacaGLOaGaayzkaaGaaiOoaiaadMhacqGH9aqpcaWG4bWaaWba % aSqabeaacaaIZaaaaOGaeyOeI0IaaG4maiaadIhadaahaaWcbeqaai % aaikdaaaGccqGHRaWkcaaIYaaaaa!4230! \left( C \right):y = {x^3} - 3{x^2} + 2\) cách đều hai điểm A(12;1),B(-6;3) .
-
Câu 33:
Cho \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9maalaaabaGaamiEaiabgUcaRiaaikdaaeaacaWG4bGaeyOeI0Ia % aGOmaaaacaaMc8UaaGPaVpaabmaabaGaam4qaaGaayjkaiaawMcaai % aac6caaaa!4361! y = \frac{{x + 2}}{{x - 2}}\,\,\left( C \right).\) Tìm M có hoành độ dương thuộc (C) sao cho tổng khoảng cách từ M đến 2 tiệm cận nhỏ nhất
-
Câu 34:
Biết \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyqamaabm % aabaGaamiEamaaBaaaleaacaWGbbaabeaakiaacUdacaaMc8UaamyE % amaaBaaaleaacaWGbbaabeaaaOGaayjkaiaawMcaaaaa!3E80! A\left( {{x_A};\,{y_A}} \right)\),\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOqamaabm % aabaGaamiEamaaBaaaleaacaWGcbaabeaakiaacUdacaaMc8UaamyE % amaaBaaaleaacaWGcbaabeaaaOGaayjkaiaawMcaaaaa!3E83! B\left( {{x_B};\,{y_B}} \right)\) là hai điểm thuộc hai nhánh khác nhau của đồ thị hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOqamaabm % aabaGaamiEamaaBaaaleaacaWGcbaabeaakiaacUdacaaMc8UaamyE % amaaBaaaleaacaWGcbaabeaaaOGaayjkaiaawMcaaaaa!3E83! B\left( {{x_B};\,{y_B}} \right)\) sao cho đoạn thẳng AB có độ dài nhỏ nhất. Tính \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuaiabg2 % da9iaadIhadaqhaaWcbaGaamyqaaqaaiaaikdaaaGccqGHRaWkcaWG % 4bWaa0baaSqaaiaadkeaaeaacaaIYaaaaOGaey4kaSIaamyEamaaBa % aaleaacaWGbbaabeaakiaac6cacaWG5bWaaSbaaSqaaiaadkeaaeqa % aaaa!439D! P = x_A^2 + x_B^2 + {y_A}.{y_B}\).
-
Câu 35:
Có bao nhiêu điểm M thuộc đồ thị hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9maalaaabaGaamiEaiabgUcaRiaaikdaaeaacaWG4bGaeyOeI0Ia % aGymaaaaaaa!3D48! y = \frac{{x + 2}}{{x - 1}}\) sao cho khoảng cách từ M đến trục tung bằng hai lần khoảng cách từ M đến trục hoành.
-
Câu 36:
Có bao nhiêu điểm thuộc đồ thị hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iabgkHiTiaadIhadaahaaWcbeqaaiaaiodaaaGccqGHsislcaaI % ZaGaamiEaiabgUcaRiaaiodaaaa!3F1C! y = - {x^3} - 3x + 3\) cách giao điểm của đồ thị hàm số với trục tung một khoảng bằng \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaOaaaeaaca % aIXaGaaG4naaWcbeaaaaa!378B! \sqrt {17} \)?
-
Câu 37:
Tìm tất cả các điểm thuộc đồ thị hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9maalaaabaGaaGOmaiaadIhacqGHRaWkcaaIXaaabaGaamiEaiab % gkHiTiaaigdaaaaaaa!3E03! y = \frac{{2x + 1}}{{x - 1}}\) có khoảng cách đến trục hoành bằng 1
-
Câu 38:
Cho hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iaadIhadaahaaWcbeqaaiaaiodaaaGccqGHsislcaaIYaGaamiE % aiabgUcaRiaaigdaaaa!3E2B! y = {x^3} - 2x + 1\). Tìm tất cả các điểm Mthuộc đồ thị hàm số sao cho khoảng cách từ M đến trục tung bằng 1.
-
Câu 39:
Hỏi có bao nhiêu cặp số nguyên dương (a;b) để hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbbG8FasPYRqj0-yi0dXdbba9pGe9xq-JbbG8A8frFve9 % Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWG5bGaey % ypa0ZaaSaaaeaacaaIYaGaamiEaiabgkHiTiaadggaaeaacaaI0aGa % amiEaiabgkHiTiaadkgaaaaaaa!3F8A! y = \frac{{2x - a}}{{4x - b}}\) có đồ thị trên \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbbG8FasPYRqj0-yi0dXdbba9pGe9xq-JbbG8A8frFve9 % Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaadaqadaqaai % aaigdacaGG7aGaaGPaVlabgUcaRiabg6HiLcGaayjkaiaawMcaaaaa % !3D3C! \left( {1;\, + \infty } \right)\) như hình vẽ dưới đây?
.png)
-
Câu 40:
A,B là hai điểm di động và thuộc hai nhánh khác nhau của đồ thị \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9maalaaabaGaaGOmaiaadIhacqGHsislcaaIXaaabaGaamiEaiab % gUcaRiaaikdaaaaaaa!3E04! y = \frac{{2x - 1}}{{x + 2}}\). Khi đó khoảng cách AB bé nhất là?
-
Câu 41:
Cho hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9maalaaabaGaamiEamaaCaaaleqabaGaaGOmaaaakiabgkHiTiaa % dIhacqGHRaWkcaaIXaaabaGaamiEaiabgkHiTiaaigdaaaaaaa!4024! y = \frac{{{x^2} - x + 1}}{{x - 1}}\) có đồ thị (C). Gọi A,B là hai điểm phân biệt trên đồ thị (C) có hoành độ \(x_1;x_2\) thỏa \(x_1<1<x_2\). Giá trị nhỏ nhất của AB là
-
Câu 42:
Hai điểm A,B thuộc hai nhánh của đồ thị \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iaaiodacqGHRaWkdaWcaaqaaiaaiEdaaeaacaWG4bGaeyOeI0Ia % aG4maaaaaaa!3D0F! y = 3 + \frac{7}{{x - 3}}\). Khi đó độ dài đoạn thẳng AB ngắn nhất bằng bao nhiêu?
-
Câu 43:
Đồ thị hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9maalaaabaGaaG4maiaadIhacqGHsislcaaIXaaabaGaaGOmaiaa % dIhacqGHRaWkcaaIXaaaaaaa!3EC0! y = \frac{{3x - 1}}{{2x + 1}}\) có tâm đối xứng là điểm.
-
Câu 44:
Đồ thị hàm số nào dưới đây có tâm đối xứng là điểm \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamysamaabm % aabaGaaGymaiaacUdacqGHsislcaaIYaaacaGLOaGaayzkaaaaaa!3B6E! I\left( {1; - 2} \right)\)?
-
Câu 45:
Đồ thị hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iaaikdacaWG4bGaey4kaSIaamyBaiabgkHiTmaalaaabaGaaGym % aaqaaiaaikdacaWG4bGaey4kaSIaaGymaaaaaaa!4093! y = 2x + m - \frac{1}{{2x + 1}}\) có tâm đối xứng là điểm
-
Câu 46:
Tâm đối xứng của đồ thị hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iaadIhadaahaaWcbeqaaiaaiodaaaGccqGHsislcaaI2aGaamiE % amaaCaaaleqabaGaaGOmaaaakiabgUcaRiaadIhacqGHRaWkcaaIXa % aaaa!4101! y = {x^3} - 6{x^2} + x + 1\) là điểm?
-
Câu 47:
Cho hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGacaGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iaadIhadaahaaWcbeqaaiaaisdaaaGccqGHsislcaaIZaGaamiE % amaaCaaaleqabaGaaGOmaaaakiabgkHiTiaaiwdaaaa!3F2E! y = {x^4} - 3{x^2} - 5\) có đồ thị (C). Điểm nào sau đây thuộc đồ thị (C)?
-
Câu 48:
Biết đồ thị hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iaadIhadaahaaWcbeqaaiaaiodaaaGccqGHsislcaaIZaGaamiE % aiabgUcaRiaaigdaaaa!3E2D! y = {x^3} - 3x + 1\) có hai điểm cực trị A, B. Khi đó phương trình đường thẳng AB là
-
Câu 49:
Cho hàm số f có đạo hàm trên khoảng I. Xét các mệnh đề sau:
(I). Nếu \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmOzayaafa % WaaeWaaeaacaWG4baacaGLOaGaayzkaaGaeyyzImRaaGimaaaa!3BF1! f'\left( x \right) \ge 0\), \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyiaIiIaam % iEaiabgIGiolaadMeaaaa!3A13! \forall x \in I\) (dấu bằng chỉ xảy ra tại một số hữu hạn điểm trên I) thì hàm số đồng biến trên I.
(II). Nếu \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmOzayaafa % WaaeWaaeaacaWG4baacaGLOaGaayzkaaGaeyizImQaaGimaaaa!3BE0! f'\left( x \right) \le 0\),\(\forall x \in I\) (dấu bằng chỉ xảy ra tại một số hữu hạn điểm trên I) thì hàm số nghịch biến trên I.
(III). Nếu \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmOzayaafa % WaaeWaaeaacaWG4baacaGLOaGaayzkaaGaeyizImQaaGimaaaa!3BE0! f'\left( x \right) \le 0; \forall x \in I\) thì hàm số nghịch biến trên khoảng I.
(IV). Nếu \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmOzayaafa % WaaeWaaeaacaWG4baacaGLOaGaayzkaaGaeyizImQaaGimaaaa!3BE0! f'\left( x \right) \le 0, \forall x \in I\) và f'(x) = 0 tại vô số điểm trên I thì hàm số f không thể nghịch biến trên khoảng I.
Trong các mệnh đề trên. Mệnh đề nào đúng, mệnh đề nào sai?
-
Câu 50:
Cho hàm số y=f(x) liên tục trên đoạn [-2;2] và có đồ thị là đường cong như trong hình vẽ bên.
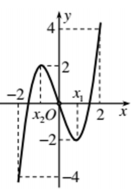
Hỏi phương trình \(|f(x)-1|=2\) có mấy nghiệm phân biệt trên [-2;2]?











