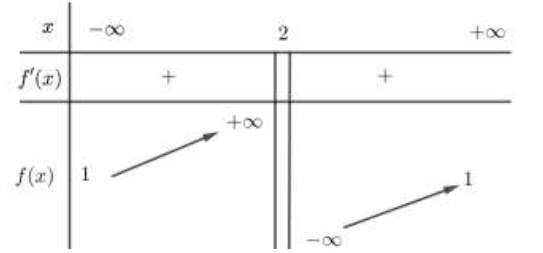
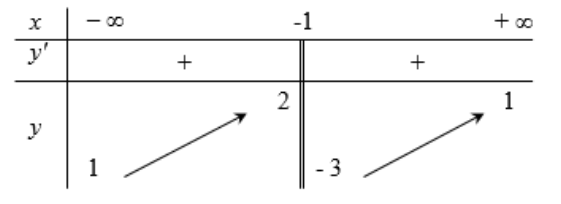
Cho hàm số \(f(x)=\frac{a x-b}{c x+b+1}(a, b, c \in \mathbb{R})\) có bảng biến thiên như sau:
Biết tập hợp tất cả các giá trị b thoả mãn là khoảng \((m: n) \text { . Tính tổng } S=m+2 n\)
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai\(\text { Đồ thị hàm số } f(x) \text { có tiệm cận ngang } y=1 \Leftrightarrow \frac{a}{-}=1 \Leftrightarrow a=c \text { . }\)
\(\text { Đồ thị hàm số } f(x) \text { có tiệm cận đứng } x=2 \Leftrightarrow-\frac{b+1}{c}=2 \Leftrightarrow c=-\frac{b+1}{2} \text { . }\)
\(\text { Hàm số } f(x) \text { đồng biến trên các khoảng xác định nên }(-\infty ; 2) ;(2 ;+\infty) \text { . }\)Từ ba điều kiện trên ta có:
\(\begin{aligned} &c(b+1)+b c>0 \Leftrightarrow c(2 b+1)>0 \Leftrightarrow-\left(\frac{b+1}{2}\right)(2 b+1)>0\\ &\Leftrightarrow(b+1)(2 b+1)<0 \Leftrightarrow-1<b<-\frac{1}{2} \Rightarrow b \in\left(-1 ;-\frac{1}{2}\right) .\\ &\text { Suy ra } m=-1 \text { và } n=-\frac{1}{2} \text { . Vậy } S=m+2 n=-1+2\left(-\frac{1}{2}\right)=-2 \text { . } \end{aligned}\)