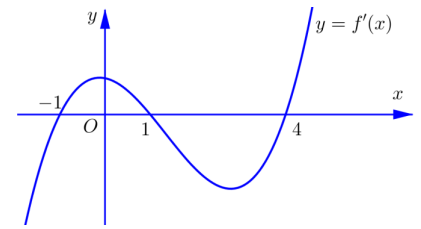
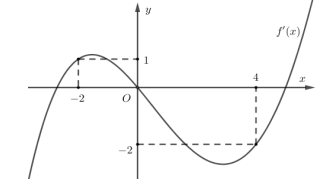
Cho hàm số \(y=f(x)\) Hàm số \(y=f'(x)\) có đồ thị như hình vẽ bên dưới. Hàm số \(g(x)=f(1-2 x)+x^{2}-x\) nghịch biến trên khoảng nào dưới đây?
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai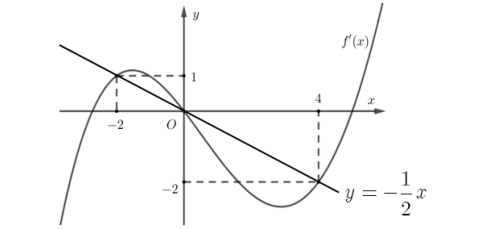
Xét hàm số \(g(x)=f(1-2 x)+x^{2}-x\)
Tập xác định:\(\mathbb{R}\)
Đạo hàm:\(g^{\prime}(x)=-2 f^{\prime}(1-2 x)+2 x-1, x \in \mathbb{R}\).
Hàm số g(x) nghịch biến khi \(g^{\prime}(x) \leq 0\).
Ta có \(g^{\prime}(x) \leq 0 \Leftrightarrow-2 f^{\prime}(1-2 x)+2 x-1 \leq 0 \Leftrightarrow f^{\prime}(1-2 x) \geq-\frac{1}{2}(1-2 x)(*)\)
Đặt \(t=1-2 x\) , bất phương trình (*) trở thành \(f^{\prime}(t) \geq-\frac{1}{2} t\)
Từ đồ thị ta có \(f^{\prime}(t) \geq-\frac{1}{2} t \Leftrightarrow\left[\begin{array}{l} -2 \leq t \leq 0 \\ t \geq 4 \end{array}\right.\)
Do đó, \(g^{\prime}(x) \leq 0 \Leftrightarrow\left[\begin{array}{l} -2 \leq 1-2 x \leq 0 \\ 1-2 x \geq 4 \end{array} \Leftrightarrow\left[\begin{array}{l} \frac{1}{2} \leq x \leq \frac{3}{2} \\ x \leq-\frac{3}{2} \end{array}\right.\right.\)
\(g^{\prime}(x)=0 \Leftrightarrow f^{\prime}(1-2 x)=-\frac{1}{2}( 1-2 x) \Leftrightarrow x \in\left\{-\frac{3}{2} ; \frac{1}{2} ; \frac{3}{2}\right\}:\)hữu hạn.
Như vậy hàm số g(x) nghịch biến trên đoạn \(\left[\frac{1}{2} ; \frac{3}{2}\right]\) và nửa khoảng \(\left(-\infty ;-\frac{3}{2}\right]\)
Xét các đáp án chọn A
.png)