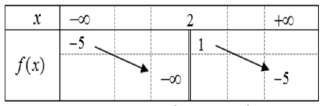
Cho hàm số y=f(x) có bảng biến thiên như hình dưới đây

Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số \(y=\frac{1}{2 f(x)-1}\) là?

Câu hỏi liên quan

• Đường tiệm cận ngang của đồ thị hàm số \(y = \dfrac{{{x^2} + 3x}}{{{x^2} - 4}}\) là:

• Số tiệm cận của đồ thị hàm số \(y=\left\{\begin{array}{l} \frac{\sqrt{x^{2}+1}}{x} \text { nếu } x \geq 1 \\ \frac{2 x}{x-1} \text { nếu } x<1 \end{array}\right.\) là

• Đồ thị hàm số \(y\; = \;\frac{{\sqrt {x + 3} }}{{\;x + 1}}\) có tất cả bao nhiêu tiệm cận?

ZUNIA12

• Số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số \(y=\frac{\sqrt{x-2}+1}{x^{2}-3 x+2}\) là?

• Có bao nhiêu giá trị m để đồ thị hàm số \(y=\frac{m x^{2}-1}{x^{2}-3 x+2}\) có đúng hai đường tiệm cận? 

• Đồ thị hàm số \(y=\frac{\sqrt{x^{2}-x+1}+m x}{x-1}\) có đường tiệm cận đứng khi 

• Tìm tất cả các giá trị của tham số m sao cho đồ thị hàm số \(y=\frac{5 x-3}{x^{2}-2 m x+1}\) không có tiệm cận
  đứng. 

• Đường thẳng nào dưới đây là tiệm cận đứng của đồ thị hàm số \(y=\frac{2 x+1}{x+1} ?\)

• Đường tiệm cận ngang của đồ thị hàm số \(y=\frac{2 x+7}{x-1}\) là:

• Đồ thị hàm số \(y = \dfrac{{5x - 1 - \sqrt {{x^2} - 2} }}{{x - 4}}\) có bao nhiêu đường tiệm cận ngang?

• Tìm mệnh đề sai trong các mệnh đề sau:

• Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số \(y=\frac{x^{2}-m x-2 m^{2}}{x-2}\) có tiệm cận đứng 

• Tập hợp tất cả các giá trị của tham số để đồ thị hàm số \(y=\frac{x-1}{x^{2}+2 m x+m}\)có ba đường tiệm cận là?

• Đồ thị của hàm số \(y=\frac{x-1}{x^{2}+2 x-3}\) có bao nhiêu đường tiệm cận?

• Đồ thị hàm số \(y=\frac{x^{2}-3 x+2}{1-x^{2}}\) có bao nhiêu đường tiệm cận ?
   

• Số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số \(y=\frac{\sqrt{x-1}+1}{x^{2}-3 x}\) là?

• Đồ thị hàm số \(y=\frac{2 x-3}{x-1}\) có các đường tiệm cận đứng và tiệm cận ngang lần lượt là:

• Đồ thị của hàm số nào dưới đây có tiệm cận ngang?x

• Biết đồ thị hàm số \(y = \frac{{\left( {2x - n} \right){x^2} + mx + 1}}{{{x^2} + mx + n - 6}}\) (m, n là tham số) nhận trục hoành và trục tung làm hai đường tiệm cận. Tính m + n 

• Đồ thị hàm số \(y=\frac{\sqrt{x^{2}-4}}{x^{2}-5 x+6}\) có tất cả bao nhiêu tiệm cận đứng và tiệm cận ngang?