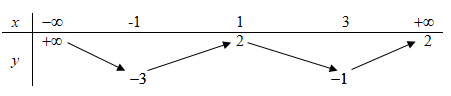
Cho hàm số y = f( x ) có bảng biến thiên như sau:

Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số\( y = \frac{1}{{f\left( x \right) - 1}}\)

Câu hỏi liên quan

• Cho hàm số \(y=\frac{2 x-3}{x-2}(C)\). Gọi d là khoảng cách từ giao điểm của 2 tiệm cận của (C) đến một tiếp tuyến bất kỳ của đồ thị (C). Giá trị lớn nhất của d là 

• Cho hàm số \(y\; = \;\frac{{mx - 1}}{{x - m}}\) với m > 1

  Hỏi giao điểm của hai đường tiệm cận của đồ thị hàm số trên luôn nằm trên một đường cố định có phương trình nào trong các phương trình sau?

• Đồ thị hàm số \(y=\frac{2 x-11}{x-1}\) có các đường tiệm cận đứng và tiệm cận ngang lần lượt là: 

ZUNIA12

• Đồ thị hàm số nào sau đây nhận đường thẳng x=2 làm đường tiệm cận:

• Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số \(y=\frac{\sqrt{x(4 x+6)}-2}{x+2}\)

• Cho hàm số \( y = \frac{{a{x^2} + 3ax + 2a + 1}}{{x + 2}}\). Chọn kết luận đúng:

• Cho hàm số y = f(x) có \(\lim\limits _{x \rightarrow+\infty} f(x)=1 \text { và } \lim\limits _{x \rightarrow-\infty} f(x)=-1\). Khẳng định nào sau đây là đúng?

• Gọi (C) là đồ thị của hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9maalaaabaGaaGOmaiaadIhacqGHsislcaaI0aaabaGaamiEaiab % gkHiTiaaiodaaaaaaa!3E12! y = \frac{{2x - 4}}{{x - 3}}\). Trong các mệnh đề sau, tìm mệnh đề sai.

• Đồ thị hàm số \(y=\frac{x-2}{x^{2}-4}\) có mấy tiệm cận?

• Đồ thị hàm số nào sau đây không có tiệm cận ngang? 

• Đường cong (C): \(y = \frac{{5x + 2}}{{{x^2} - 4}}\) có bao nhiêu tiệm cận?

• Hàm số \(y = \frac{{2x - 1}}{{x - 1}}{\mkern 1mu} {\mkern 1mu} \left( H \right)\). Gọi M là một điểm bất kì thuộc (H). Tiếp tuyến với (H) tại M tạo với hai đường tiệm cận một tam giác có diện tích bằng:

• Đồ thị của hàm số \(y = \frac{{x + 1}}{{{x^2} + 2x - 3}}\) có bao nhiêu tiệm cận ?

• Tìm giá trị m để hai đường tiệm cận của đồ thị hàm số \(y = \frac{{mx + 2}}{{3 - 2x}}\) (m khác \(\frac{{ - 4}}{3}\))tạo với hai trục tọa độ một hình chữ nhật có diện tích bằng 1/5 

• Đồ thị hàm số \(y=\frac{2 x-1}{x+2}\) có bao nhiêu đường tiệm cận

• Đồ thị hàm số \(y = \dfrac{{2x - 1}}{{x + 2}}\) có đường tiệm cận ngang là đường thẳng nào sau đây?

• Với giá trị nào của m thì đồ thị \((\mathrm{C}): y=\frac{m x-1}{2 x+m}\) có tiệm cận đứng đi qua điểm \(M(-1 ; \sqrt{2}) ?\)

• Đường tiệm cận ngang của đồ thị hàm số \(y = \dfrac{{3x + 1}}{{3 - 2x}}\) là:

• Số tiệm cận đứng của đồ thị hàm số \(y=\frac{\sqrt{x+16}-4}{x^{2}+x}\) là:

• Đồ thị của hàm số nào dưới đây có tiệm cận đứng?