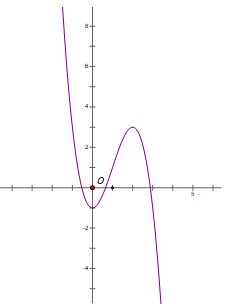
Cho hàm số y=f(x) có đồ thị như hình vẽ sau:
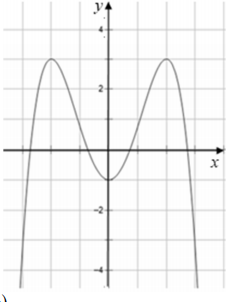
Số nghiệm của phương trình \(\frac{1-f(x)}{1+f(x)}=2\) là?
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo saiTa có: \(\frac{1-f(x)}{1+f(x)}=2 \Rightarrow 1-f(x)=2+2 f(x) \Leftrightarrow f(x)=-\frac{1}{3}\)
Số nghiệm của phương tình là số giao điểm của đồ thị hai hàm sốy=f(x) và \(y={-1\over3}\).
Dựa vào đồ thị hàm số ta thấy đồ thị hàm số y=f(x) và đồ thị hàm số \(y={-1\over3}\) cắt nhau tại 4 điểm phân biệt nên \(\frac{1-f(x)}{1+f(x)}=2\) có 4 nghiệm phân biệt.
ADMICRO
YOMEDIA
ZUNIA9
.png)
.png)











