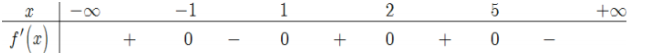Cho hàm số y = f(x) = x4+ 2mx2+ m. Tìm m để f(x) > 0 với mọi m.
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTheo đầu bài:
y = f(x) = x4+ 2mx2+ m > 0 với mọi x
\(\begin{array}{l}
\Leftrightarrow m\left( {2{x^2} + 1} \right) > - {x^4}\\
\Leftrightarrow m > \frac{{ - {x^4}}}{{2{x^2} + 1}}\forall x\left( * \right)
\end{array}\)
Xét
\(\begin{array}{l}
g\left( x \right) = \frac{{ - {x^4}}}{{2{x^2} + 1\;}}\\
g'\left( x \right) = \frac{{ - 4{x^3}\left( {2{x^2} + 1} \right) + 4{x^5}}}{{{{\left( {2{x^2} + 1\;} \right)}^2}}} = \frac{{ - 4{x^5} - 4{x^3}}}{{{{\left( {2{x^2} + 1\;} \right)}^2}}} = \frac{{ - 4{x^3}\left( {1 + {x^2}} \right)}}{{{{\left( {2{x^2} + 1\;} \right)}^2}}}
\end{array}\)
Phương trình g’(x) =0 khi và chỉ khi x = 0
Bảng biến thiên
Dựa vào bảng biến thiên từ (*) suy ra m > 0.
Câu hỏi liên quan
-
Trong các hình trụ nội tiếp hình cầu bán kính R, hãy tìm hình trụ có thể tích lớn nhất.
-
Tập hợp các giá trị thực của m để hàm số \(y=\frac{-3 x^{2}+m x-2}{2 x-1}\) luôn nghịch biến trên từng khoảng xác định là
-
Hàm số \(y = x ⁴ - 1\) đồng biến trên khoảng nào dưới đây?
-
Cho hàm số f(x) có bảng xét dấu đạo hàm f'(x) như sau:
Hàm số \(y=3 f(-x+2)+e^{x^{3}+3 x^{2}-9 x+1}\) nghịch biến trên khoảng nào dưới đây?
-
Tìm tất cả các giá trị thực của tham số m sao cho hàm số \(y=\frac{1}{3} x^{3}-\frac{1}{2} m x^{2}+2 m x-3 m+4\) nghịch biến trên một đoạn có độ dài là 3?
-
Trong tất cả các giá trị của tham số m để hàm số \(y=\frac{1}{3}x^3+mx^2–mx–m \) đồng biến trên R, giá trị nhỏ nhất của m là?
-
Hàm số \(y = {x^2} + 2x\) nghịch biến trên các khoảng:
-
Khoảng đồng biến của hàm số \(y=x^4-2x^2+1\) là
-
Cho đồ thị hàm số y = −x3 như hình vẽ. Hàm số y = −x3 nghịch biến trên khoảng:
-
Hàm số \(y = \frac{1}{3}{x^3} - 3{x^2} + 1\) nghịch biến trên các khoảng:
-
Cho hàm số \(f(x)=\frac{(m-1) x-1}{m x+2 m+1}\). Tìm giá trị nguyên của m để hàm số nghịch biến trên khoảng \((0 ;+\infty) ?\)
-
Số giá trị nguyên của tham số m để hàm số \(y=\left(4-m^{2}\right) x^{3}+(m-2) x^{2}+x+m-1(1)\) đồng biến trên \(\mathbb{R}\) là
-
Tổng các giá trị nguyên của \(m \in[-25 ; 25]\) để hàm số \(y=\frac{(2 m+1) \tan x+1}{\tan x+m}\) đồng biến trên khoảng \(\left(0 ; \frac{\pi}{2}\right)\) là
-
Tính tổng các giá trị nguyên của tham số m trên khoảng (-2020; 2020 ) để hàm số \(y=\frac{\sin x-3}{\sin x-m}\)đồng biến trên khoảng \(\left(0 ; \frac{\pi}{4}\right)\).
-
Cho hàm số y = f (x) có đồ thị như hình vẽ. Khi đó f (x ) đồng biến trên các khoảng nào?
-
Hàm số \(y = - {x^3} - 2{x^2} + 3x\) đồng biến trên các khoảng:
-
Hàm số \(y = - 2{x^3} + 3{x^2} - 3\) nghịch biến trên các khoảng:
-
Hàm số \(y = \frac{1}{3}{x^3} + {x^2} - x\) nghịch biến trên khoảng nào sau đây?
-
Hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iaadIhadaahaaWcbeqaaiaaiodaaaGccqGHsislcaWG4bWaaWba % aSqabeaacaaIYaaaaOGaeyOeI0IaamiEaiabgUcaRiaaiodaaaa!404F! y = {x^3} - {x^2} - x + 3\) nghịch biến trên khoảng
-
Cho hàm số y = x4 – 2x2 + 3. Tìm các khoảng đồng biến của hàm số
