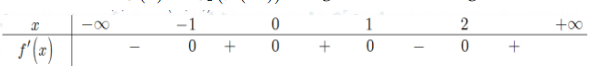Cho hàm số y=f(x) có bảng xét dấu của đạo hàm như sau

Đặt \(g(x)=f\left(\frac{x-1}{2}\right)-\frac{1}{3} x^{3}+\frac{3}{2} x^{2}-2 x+3\) . Mệnh đề nào dưới đây sai?
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai\(g^{\prime}(x)=\frac{1}{2} f^{\prime}\left(\frac{x-1}{2}\right)-x^{2}+3 x-2=\frac{1}{2}\left[f^{\prime}\left(\frac{x-1}{2}\right)-2 x^{2}+6 x-4\right]\)
Hàm số nghịch biến khi:
\(g^{\prime}(x)<0 \Rightarrow f^{\prime}\left(\frac{x-1}{2}\right)-2 x^{2}+6 x-4<0\)
\(\Rightarrow\left\{\begin{array}{l} -2 x^{2}+6 x-4<0 \\ f^{\prime}\left(\frac{x-1}{2}\right)<0 \end{array}\right.\)
\(\left\{ \begin{array}{l} \left[ {\begin{array}{*{20}{l}} {x < 1}\\ {x > 2} \end{array}} \right.\\ \left[ {\begin{array}{*{20}{l}} { - \frac{5}{2} < \frac{{x - 1}}{2} < \frac{1}{2}}\\ {\frac{{x - 1}}{2} > 3} \end{array}} \right. \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} \left[ {\begin{array}{*{20}{l}} {x < 1}\\ {x > 2} \end{array}} \right.\\ \left[ {\begin{array}{*{20}{l}} { - 4 < x < 2}\\ {x > 7} \end{array}} \right. \end{array} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}} { - 4 < x < 1}\\ {x > 7} \end{array}} \right.\)
Từ các đáp án suy ra B sai.