Cho hình chóp S ABCD . có đáy ABCD là hình chữ nhật, cạnh bên SA vuông góc với đáy, \(A B=a, A D=2 a, S A=3 a\) . Gọi M, N lần lượt là hình chiếu của A lên SB, SD và P là giao điểm của SC với mặt phẳng \((A M N)\) . Tính thể tích khối chóp S AMPN?
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
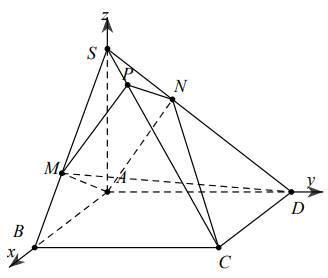
Báo saiChọn hệ trục tọa độ như hình vẽ.
\(\begin{aligned} &\text { Ta có tọa độ các điểm } A(0 ; 0 ; 0), B(a ; 0 ; 0), D(0 ; 2 a ; 0), C(a ; 2 a ; 0), S(0 ; 0 ; 3 a) \text { . }\\ &\text { Suy ra } \overrightarrow{S B}=(a ; 0 ;-3 a), \overrightarrow{S D}=(0 ; 2 a ;-3 a), \overrightarrow{S C}=(a ; 2 a ;-3 a)\\ &\text { Phương trình } S B:\left\{\begin{array}{l} x=a+t \\ y=0 \\ z=-3 t \end{array}\right.\\ &\Rightarrow M(a+t ; 0 ;-3 t) \Rightarrow \overrightarrow{A M}=(a+t ; 0 ;-3 t)\\ &\text { Mà } A M \perp S B \Rightarrow \overrightarrow{A M} \cdot \overrightarrow{S B}=0 \Leftrightarrow(a+t)+9 t=0 \Rightarrow t=\frac{-a}{10} \Rightarrow M\left(\frac{9 a}{10} ; 0 ; \frac{3 a}{10}\right)\\ &\text { Tương tự vậy ta tìm được } N\left(0 ; \frac{18 a}{13} ; \frac{12 a}{13}\right) \text { . } \end{aligned}\)
\(\begin{aligned} &\text { Suy ra } \overrightarrow{n_{1}}=[\overrightarrow{A M}, \overrightarrow{A N}]=-\frac{27 a^{2}}{65}(1 ; 2 ;-3) \text { . }\\ &\text { Do đó ta có phương trình của }(A M N): x+2 y-3 z=0 \text { . } \end{aligned}\)
\(\text { Phương trình } S C:\left\{\begin{array}{l} x=t \\ y=2 t \\ z=3 a-3 t \end{array}\right.\) nên tọa độ điểm P là nghiệm của hệ
\(\begin{array}{l} \left\{\begin{array}{l} x=t \\ y=2 t \\ z=3 a-3 t \\ x+2 y-3 z=0 \end{array} \Rightarrow x=\frac{9 a}{14}, y=\frac{9 a}{7}, z=\frac{15 a}{14} \Rightarrow P\left(\frac{9 a}{14} ; \frac{9 a}{7} ; \frac{15 a}{14}\right)\right. \\ \text { Ta có: }[\overrightarrow{A M}, \overrightarrow{A P}]=-\frac{27 a^{2}}{70}(1 ; 2 ;-3),[\overrightarrow{A N}, \overrightarrow{A P}]=\frac{27 a^{2}}{91}(1 ; 2 ;-3) \\ \text { Suy ra } S_{A M P N}=\frac{1}{2}[|[\overrightarrow{A M}, \overrightarrow{A P}]|+|[\overrightarrow{A N}, \overrightarrow{A P}]|]=\frac{621 \sqrt{14} \cdot a^{2}}{1820} \text { và } d(S,(A M N))=\frac{9 a}{\sqrt{14}} \text { . } \\ \text { Vậy } V_{S . A M P N}=\frac{1}{3} \cdot \frac{9 a}{\sqrt{14}} \cdot \frac{621 \sqrt{14} \cdot a^{2}}{1820}=\frac{1863 \cdot a^{3}}{1820} . \end{array}\)
.png)











