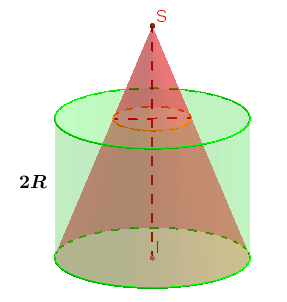
Cho hình nón có độ dài đường kính đáy là \(2R\), độ dài đường sinh là \(R\sqrt{17}\) và hình trụ có chiều cao và đường kính đáy đều bằng \(2R\), lồng vào nhau như hình vẽ.
Tính thể tích phần khối trụ không giao với khối nón
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai.PNG)
Ta có \(SI=\sqrt{S{{B}^{2}}-I{{B}^{2}}}=\sqrt{17{{R}^{2}}-{{R}^{2}}}=4R\Rightarrow SE=2R,EF=\frac{R}{2}\).
Thể tích khối nón lớn (có đường cao \(SI\)) là \({{V}_{1}}=\frac{1}{3}\pi {{R}^{2}}.4R=\frac{4}{3}\pi {{R}^{3}}\).
Thể tích khối nón nhỏ (có đường cao \(SE\)) là \({{V}_{2}}=\frac{1}{3}\pi {{\left( \frac{R}{2} \right)}^{2}}.2R=\frac{1}{6}\pi {{R}^{3}}\)
Thể tích phần khối giao nhau giữ khối nón và khối trụ là \({{V}_{3}}={{V}_{1}}-{{V}_{2}}{{V}_{2}}=\frac{7}{6}\pi {{R}^{3}}\).
Thể tích khối trụ là là \({{V}_{4}}=\pi {{R}^{2}}.2R=2\pi {{R}^{3}}\).
Vậy thể tích phần khối trụ không giao với khối nón là \(V={{V}_{4}}-{{V}_{3}}=\frac{5}{6}\pi {{R}^{3}}\).
Câu hỏi liên quan
-
Một hình nón có đường kính của đường tròn đáy bằng 10 (cm) và chiều dài của đường sinh bằng 15 (cm). Thể tích của khối nón bằng.
-
Cắt khối trụ bởi một mặt phẳng qua trục ta được thiết diện là hình chữ nhật ABCD có AB và CD thuộc hai đáy của hình trụ, AB = 4a, AC = 5a. Tính thể tích khối trụ.
-
Cho hình trụ có bán kính đáy \(5\,cm\), chiều cao \(4\,cm\). Diện tích toàn phần của hình trụ này là
-
Cho một hình trụ có bán kính đáy R, chiều cao h và thể tích V1; một hình nón có đáy trùng với một đáy của hình trụ, có đỉnh trùng với tâm đáy còn lại của hình trụ (hình vẽ bên dưới) và có thể tích V2.
Khẳng định nào sau đây là khẳng định đúng ?
.png)
-
Cho hình nón có bán kính đáy là 4a, chiều cao là 3a. Diện tích toàn phần hình nón là
-
Một chiếc phễu đựng dầu hình nón có chiều cao là 30cm và đường sinh là 50cm. Giả sử rằng lượng dầu mà chiếc phễu đựng được chính là thể tích của khối nón. Khi đó trong các lượng dầu sau đây, lượng dầu nào lớn nhất chiếc phễu có thể đựng được:
-
Nếu cắt mặt trụ tròn xoay bởi một mặt phẳng tạo với trục một góc \(\alpha ( 0^0 <\alpha < 90^0 )\) thì ta được:
-
Cho hình chữ nhật ABCD có AC = 2AD = 2a. Quay quanh trục AB đường gấp khúc ADCB ta được hình trụ có diện tích xung quanh là:
-
Một khối nón có thể tích bằng \(4\pi\) và chiều cao là 3 . Bán kính đường tròn đáy của hình nón là
-
Một hình trụ có bán kính đáy r = a, độ dài đường sinh \(l = 2a\). Diện tích toàn phần của hình trụ này là:
-
Cho hình nón có đường cao bằng 2a và đường sinh bằng \(a\sqrt 5 \). Tính diện tích toàn phần của hình nón.
-
Hình ABCD khi quay quanh BC thì tạo ra:
-
Cắt một khối trụ cho trước bởi một mặt phẳng vuông góc với trục thì được hai khối trụ mới có tổng diện tích toàn phần nhiều hơn diện tích toàn phần của khối trụ ban đầu \(18\pi \,\left( {d{m^2}} \right)\). Biết chiều cao của khối trụ ban đầu là \(5\,\left( {dm} \right)\), tính tổng diện tích toàn phần S của hai khối trụ mới.
-
Một cái phễu có dạng hình nón. Chiều cao của phễu là 20 cm. Người ta đổ một lượng nước vào phễu sao cho chiều cao của cột nước trong phễu bằng 10 cm (Hình H1). Nếu bịt kín miệng phễu rồi lật ngược phễu lên (Hình H2) thì chiều cao của cột nước trong phễu gần bằng với giá trị nào sau đây ?
-
Cho hình chữ nhật (ABCD ) có (AB = 4 ) và (AD = 3. ) Thể tích của khối trụ được tạo thành khi quay hình chữ nhật (ABCD ) quanh cạnh (AB ) bằng
-
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a2a và đường cao \(SA = a\sqrt 3 .\). Mặt phẳng (P) vuông góc với SA tại trung điểm M của SA cắt SB, SC, SD lần lượt tại N,P,Q. Xét hình trụ có đáy là đường tròn ngoại tiếp MNPQ và đường sinh MA thì thể tích khối trụ này có giá trị là
-
Cho hình chữ nhật ABCD có AB = 2AD. Lần lượt quay hình chữ nhật quanh các trục AB, AD ta được hai khối trụ lần lượt gọi là (H1), (H2). Tính tỉ số thể tích của khối trụ (H1) chia cho thể tích của khối trụ (H2)
-
Cho hình vẽ sau, chọn mệnh đề sai:
-
Cho tam giác ABC vuông tại A có AB = 6,AC = 8. Tính diện tích xung quanh của hình nón tròn xoay tạo thành khi quay tam giác ABC quanh cạnh AC.
-
Một hình tứ diện đều cạnh a có một đỉnh trùng với đỉnh của hình nón tròn xoay còn ba đỉnh còn lại của tứ diện nằm trên đường tròn đáy của hình nón. Diện tích xung quanh của hình nón tròn xoay là:
