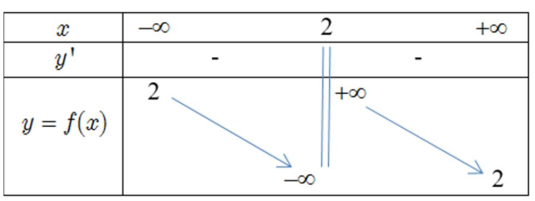
Tìm các giá trị của tham số m sao cho hàm số \(y=\frac{x+1}{x+m}\) nghịch biến trên khoảng \((2 ;+\infty) .\)
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo sai\(\begin{array}{l} D=\mathbb{R} \backslash\{-m\} ; y^{\prime}=\frac{m-1}{(x+m)^{2}}\\ \text { Theo yêu cầu bài toán: }\\ y^{\prime}<0, \forall x \in(2 ;+\infty) \Leftrightarrow \frac{m-1}{(x+m)^{2}}<0, \forall x \in(2 ;+\infty) \Leftrightarrow\left\{\begin{array} { l } { m - 1 < 0 } \\ { - m \notin ( 2 ; + \infty ) } \end{array} \Leftrightarrow \left\{\begin{array}{l} m<1 \\ -m \leq 2 \end{array} \Leftrightarrow-2 \leq m<1 .\right.\right. \end{array}\)
ADMICRO
YOMEDIA
ZUNIA9