Tìm tất cả các giá trị của tham số m để hàm số \(y=x^{3}-6 x^{2}+m x+3\) đồng biến trên khoảng \((0 ;+\infty)\)?
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai\(y^{\prime}=3 x^{2}-12 x+m\)
\(\text { Hàm số đã cho đồng biến trên khoảng }(0 ;+\infty) \text { khi và chỉ khi } y^{\prime} \geq 0 \text { , với mọi } x \in(0 ;+\infty)\)
\(\Leftrightarrow m \geq-3 x^{2}+12 x, \forall x>0 \Leftrightarrow m \geq \max _{x \in(0 ;+\infty)}\left\{-3 x^{2}+12 x\right\} .\)
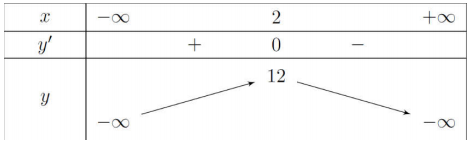
\(\begin{array}{l} \text { Xét } f(x)=-3 x^{2}+12 x \text { với } x>0 \text { . } \\ \text { Ta có } f^{\prime}(x)=-6 x+12 ; f^{\prime}(x)=0 \Leftrightarrow x=2 \text { . } \end{array}\)
Bảng biến thiên
Dựa vào bảng biến thiên, ta được giá trị m thỏa mãn yêu cầu bài toán là \(m \geq 12 \text { , }\)