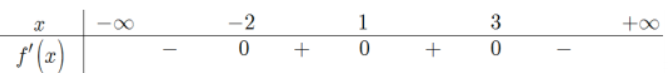Cho hàm số y=f(x) liên tục trên [-2;4] và có bảng biến thiên như hình vẽ
Có bao nhiêu giá trị nguyên của tham số m để phương trình \(f(3 \cos x+1)=-\frac{m}{2}\) có nghiệm?
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo saiTa có \(-1 \leq \cos x \leq 1 \Rightarrow-2 \leq 3 \cos x+1 \leq 4\)
Đặt \(t=3 \cos x+1\), khi đó để phương trình \(f(3 \cos x+1)=-\frac{m}{2}\) có nghiệm thì phương trình \(f(t)=-\frac{m}{2}\) có nghiệm \(t \in[-2 ; 4]\) .
Từ bảng biến thiên suy ra yêu cầu bài toán 1\(\Leftrightarrow-1 \leq-\frac{m}{2} \leq 3 \Leftrightarrow-6 \leq m \leq 2\) .
Do \(m \in \mathbb{Z} \Rightarrow m \in\{-6 ;-5 ;-4 ;-3 ;-2-1 ; 0 ; 1 ; 2\}\) .
Vậy, có tất cả 9 giá trị thỏa mãn.
ADMICRO
YOMEDIA
ZUNIA9