Trắc nghiệm Hàm số lũy thừa Toán Lớp 12

Câu 1:

Cho x = 2000! . Giá trị của biểu thức \(A\; = \;\frac{1}{{{{\log }_2}x}} + \frac{1}{{{{\log }_3}x}} + ... + \frac{1}{{{{\log }_{2000}}x}}\) là:

Câu 2:

Điều kiện xác định của biểu thức  \(T\; = \lg \sqrt {\left( {{x^2} - 4} \right)\left( {{x^2} - 6x + 9} \right)} \) là

Câu 3:

Với giá trị nào của x thì biểu thức:  f(x) = log₅( x³-x²-2x) xác định?

Câu 4:

Với giá trị nào của x thì biểu thức: f( x) = log₆( 2x- x²)  xác định?

Câu 5:

Với giá trị nào của x thì biểu thức \(A\; = \;{\log _{\frac{1}{2}}}\frac{{x - 1}}{{3 + x}}\) xác định?

Câu 6:

Với giá trị nào của x thì biểu thức C = ln( 4- x²) xác định?

Câu 7:

Trong các biểu thức sau biểu thức nào không có nghĩa

Câu 8:

Với giá trị nào của thì đẳng thức \(\sqrt[4]{{{x^4}}} = \frac{1}{{\left| x \right|}}\) đúng

Câu 9:

Tìm biểu thức không có nghĩa trong các biểu thức sau:

Câu 10:

Tìm x để biểu thức \({\left( {{x^2} + x + 1} \right)^{ - \frac{2}{3}}}\) có nghĩa:

Câu 11:

Tìm tập xác định D của hàm số \(y = {\left( {{x^2} - 6x + 8} \right)^{\sqrt 2 }}\)

Câu 12:

Tìm x để biểu thức (2x - 1)^{– 2}  có nghĩa:

Câu 13:

Tìm tập xác định D của hàm số y = ( x³ - 8) ^-100

Câu 14:

Tìm tập xác định D của hàm số y = (x² - 3x + 2)¹⁰⁰ 

Câu 15:

 Cho \(\alpha, \beta\) là các số thực. Đồ thị các hàm số \(y=x^{\alpha}, y=x^{\beta}\) , trên khoảng \((0 ;+\infty)\) được cho trong hình vẽ bên. Khẳng định nào sau đây là đúng?

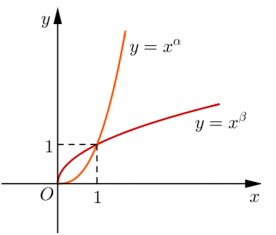
Câu 16:

Cho hàm số \(y=x^{-\sqrt{2}}\) . Mệnh đề nào sau đây là sai?

Câu 17:

 Cho hàm số \(y=x^{e-3}\) trong các kết luận sau kết luận nào sai?

Câu 18:

 Cho hàm số\(y=x^{-\sqrt{2017}}\). Mệnh đề nào dưới đây là đúng về đường tiệm cận của đồ thị hàm số?

Câu 19:

Hình vẽ bên là đồ thị các hàm số \(y=x^{a}, y=x^{b}, y=x^{c} \text { trên miền }(0 ;+\infty)\). Hỏi trong các số a , b , c số nào nhận giá trị trong khoảng  (0; 1) ?

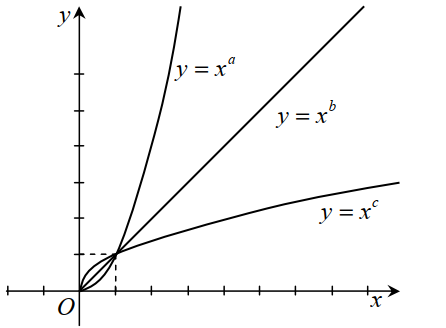
Câu 20:

Hàm số nào trong hàm số sau đây có đồ thị phù hợp với hình vẽ bên?

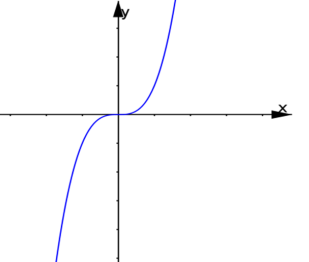
Câu 21:

Cho hai số thực x , y thỏa mãn \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac+ % gacaGGNbWaaSbaaSqaaiaadIhadaahaaadbeqaaiaaikdaaaWccqGH % RaWkcaWG5bWaaWbaaWqabeaacaaIYaaaaaWcbeaakmaabmaabaGaam % iEaiabgUcaRiaadMhaaiaawIcacaGLPaaacqGHLjYScaaIXaaaaa!44A8! {\log _{{x^2} + {y^2}}}\left( {x + y} \right) \ge 1\). Tìm giá trị lớn nhất của biểu thức S = x+2y.

Câu 22:

Cho hai số thực dương a,b thỏa mãn \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVCsPYR2xbba9asFD0dXdHaVhbbf9v8qqaqFr0xc9pk % 0xbba9q8WqFfea0-yr0RYxir-Jbba9q8aq0-yq-He9q8qqQ8frFve9 % Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGHbWaaW % baaSqabeaacaaIYaaaaOGaey4kaSIaamOyamaaCaaaleqabaGaaGOm % aaaakiabg6da+iaaigdaaaa!3EE1! {a^2} + {b^2} > 1\) và \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVCsPYR2xbba9asFD0dXdHaVhbbf9v8qqaqFr0xc9pk % 0xbba9q8WqFfea0-yr0RYxir-Jbba9q8aq0-yq-He9q8qqQ8frFve9 % Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaaciGGSbGaai % 4BaiaacEgadaWgaaWcbaGaamyyamaaCaaameqabaGaaGOmaaaaliab % gUcaRiaadkgadaahaaadbeqaaiaaikdaaaaaleqaaOWaaeWaaeaaca % WGHbGaey4kaSIaamOyaaGaayjkaiaawMcaaiabgwMiZkaaigdaaaa!46E1! {\log _{{a^2} + {b^2}}}\left( {a + b} \right) \ge 1\). Tìm giá trị lớn nhất của biểu thức P = 2a + 4b - 3.

Câu 23:

Cho hai số thực x,y thỏa mãn \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac+ % gacaGGNbWaaSbaaSqaaiaadIhadaahaaadbeqaaiaaikdaaaWccqGH % RaWkcaWG5bWaaWbaaWqabeaacaaIYaaaaSGaey4kaSIaaGOmaaqaba % GcdaqadaqaaiaadIhacqGHRaWkcaWG5bGaey4kaSIaaG4maaGaayjk % aiaawMcaaiabgwMiZkaaigdaaaa!47E5! {\log _{{x^2} + {y^2} + 2}}\left( {x + y + 3} \right) \ge 1\). Tìm giá trị lớn nhất của biểu thức S = 3x +4y -6.

Câu 24:

Cho hai số thực x,y thỏa mãn \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEamaaCa % aaleqabaGaaGOmaaaakiabgUcaRiaadMhadaahaaWcbeqaaiaaikda % aaGccqGH+aGpcaaIXaaaaa!3C7A! {x^2} + {y^2} > 1\) và \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac+ % gacaGGNbWaaSbaaSqaaiaadIhadaahaaadbeqaaiaaikdaaaWccqGH % RaWkcaaIYaGaamyEamaaCaaameqabaGaaGOmaaaaaSqabaGcdaqada % qaaiaaikdacaWG4bGaey4kaSIaamyEaaGaayjkaiaawMcaaiabgwMi % Zkaaigdaaaa!4620! {\log _{{x^2} + 2{y^2}}}\left( {2x + y} \right) \ge 1\). Biết giá trị lớn nhất của P = x+y là \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca % WGHbGaey4kaSIaamOyamaakaaabaGaaGOnaaWcbeaaaOqaaiaadoga % aaaaaa!3A80! \frac{{a + b\sqrt 6 }}{c}\) với a,b,c là các số nguyên dương và \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca % WGHbaabaGaam4yaaaaaaa!37D2! \frac{a}{c}\) tối giản. Tính S = a+ b+ c

Câu 25:

Số thực a nhỏ nhất để bất đẳng thức \(ln(1+x)\ge x - ax^2\) luôn đúng với mọi số thực dương x là \(\frac{m}{n}\) với m,n là các số nguyên dương và \(\frac{m}{n}\) tối giản. Tính

T = 2m+3n.

Câu 26:

Tất cả các giá trị thực của m để bất phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEamaaka % aabaGaamiEaaWcbeaakiabgUcaRmaakaaabaGaamiEaiabgUcaRiaa % igdacaaIYaaaleqaaOGaeyizImQaamyBaiaac6caciGGSbGaai4Bai % aacEgadaWgaaWcbaGaaGynaiabgkHiTmaakaaabaGaaGinaiabgkHi % TiaadIhaaWqabaaaleqaaOGaaG4maaaa!4807! x\sqrt x + \sqrt {x + 12} \le m.{\log _{5 - \sqrt {4 - x} }}3\) có nghiệm là

Câu 27:

Trong tất cả các cặp (x;y) thỏa mãn \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac+ % gacaGGNbWaaSbaaSqaaiaadIhadaahaaadbeqaaiaaikdaaaWccqGH % RaWkcaWG5bWaaWbaaWqabeaacaaIYaaaaSGaey4kaSIaaGOmaaqaba % GcdaqadaqaaiaaisdacaWG4bGaey4kaSIaaGinaiaadMhacqGHsisl % caaI0aaacaGLOaGaayzkaaGaeyyzImRaaGymaaaa!496D! {\log _{{x^2} + {y^2} + 2}}\left( {4x + 4y - 4} \right) \ge 1\). Tìm m để tồn tại duy nhất cặp (x,y) sao cho \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEamaaCa % aaleqabaGaaGOmaaaakiabgUcaRiaadMhadaahaaWcbeqaaiaaikda % aaGccqGHRaWkcaaIYaGaamiEaiabgkHiTiaaikdacaWG5bGaey4kaS % IaaGOmaiabgkHiTiaad2gacqGH9aqpcaaIWaaaaa!4536! {x^2} + {y^2} + 2x - 2y + 2 - m = 0\).

Câu 28:

Trong các nghiệm ( x ; y ) thỏa mãn bất phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac+ % gacaGGNbWaaSbaaSqaaiaadIhadaahaaadbeqaaiaaikdaaaWccqGH % RaWkcaaIYaGaamyEamaaCaaameqabaGaaGOmaaaaaSqabaGccaGGOa % GaaGOmaiaadIhacqGHRaWkcaWG5bGaaiykaiabgwMiZkaaigdaaaa!45EF! {\log _{{x^2} + 2{y^2}}}(2x + y) \ge 1\). Giá trị lớn nhất của biểu thức T = 2x + y bằng:

Câu 29:

Tập nghiệm của bất phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaaca % aIYaWaaWbaaSqabeaacaWG4bWaaWbaaWqabeaacaaIYaaaaSGaeyOe % I0IaaGinaaaakiabgkHiTiaaigdaaiaawIcacaGLPaaacaGGUaGaci % iBaiaac6gacaWG4bWaaWbaaSqabeaacaaIYaaaaOGaeyipaWJaaGim % aaaa!43F9! \left( {{2^{{x^2} - 4}} - 1} \right).\ln {x^2} < 0\) là

Câu 30:

Bất phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciyBaiaacg % gacaGG4bWaaiWaaeaaciGGSbGaai4BaiaacEgadaWgaaWcbaGaaG4m % aaqabaGccaWG4bGaai4oaiGacYgacaGGVbGaai4zamaaBaaaleaada % WcaaqaaiaaigdaaeaacaaIYaaaaaqabaGccaWG4baacaGL7bGaayzF % aaGaeyipaWJaaG4maaaa!47C3! \max \left\{ {{{\log }_3}x;{{\log }_{\frac{1}{2}}}x} \right\} < 3\) có tập nghiệm là.

Câu 31:

Tìm tập xác định hàm số sau \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOzamaabm % aabaGaamiEaaGaayjkaiaawMcaaiabg2da9maakaaabaGaciiBaiaa % c+gacaGGNbWaaSbaaSqaamaalaaabaGaaGymaaqaaiaaikdaaaaabe % aakmaalaaabaGaaG4maiabgkHiTiaaikdacaqG4bGaeyOeI0IaamiE % amaaCaaaleqabaGaaGOmaaaaaOqaaiaadIhacqGHRaWkcaaIXaaaaa % Wcbeaaaaa!47FA! f\left( x \right) = \sqrt {{{\log }_{\frac{1}{2}}}\frac{{3 - 2{\rm{x}} - {x^2}}}{{x + 1}}} \)

Câu 32:

Gọi \(S_1,S_2,S_3\) lần lượt là tập nghiệm của các bất phương trình sau: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaGOmamaaCa % aaleqabaGaamiEaaaakiabgUcaRiaaikdacaGGUaGaaG4mamaaCaaa % leqabaGaamiEaaaakiabgkHiTiaaiwdadaahaaWcbeqaaiaadIhaaa % GccqGHRaWkcaaIZaGaeyOpa4JaaGimaaaa!4265! {2^x} + {2.3^x} - {5^x} + 3 > 0\) \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac+ % gacaGGNbWaaSbaaSqaaiaaikdaaeqaaOWaaeWaaeaacaWG4bGaey4k % aSIaaGOmaaGaayjkaiaawMcaaiabgsMiJkabgkHiTiaaikdaaaa!4137! ;{\log _2}\left( {x + 2} \right) \le - 2\) \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaada % WcaaqaaiaaigdaaeaadaGcaaqaaiaaiwdaaSqabaGccqGHsislcaaI % XaaaaaGaayjkaiaawMcaamaaCaaaleqabaGaamiEaaaakiabg6da+i % aaigdaaaa!3DCA! ; {\left( {\frac{1}{{\sqrt 5 - 1}}} \right)^x} > 1\).Tìm khẳng định đúng?

Câu 33:

Tập nghiệm của bất phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac6 % gadaWadaqaamaabmaabaGaamiEaiabgUcaRiaaigdaaiaawIcacaGL % PaaadaqadaqaaiaadIhacqGHsislcaaIYaaacaGLOaGaayzkaaWaae % WaaeaacaWG4bGaeyOeI0IaaG4maaGaayjkaiaawMcaaiabgUcaRiaa % igdaaiaawUfacaGLDbaacqGH+aGpcaaIWaaaaa!49AB! \ln \left[ {\left( {x + 1} \right)\left( {x - 2} \right)\left( {x - 3} \right) + 1} \right] > 0\) là

Câu 34:

Tập nghiệm của bất phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac6 % gadaWadaqaamaabmaabaGaamiEaiabgkHiTiaaigdaaiaawIcacaGL % PaaadaqadaqaaiaadIhacqGHsislcaaIYaaacaGLOaGaayzkaaWaae % WaaeaacaWG4bGaeyOeI0IaaG4maaGaayjkaiaawMcaaiabgUcaRiaa % igdaaiaawUfacaGLDbaacqGH+aGpcaaIWaaaaa!49B6! \ln \left[ {\left( {x - 1} \right)\left( {x - 2} \right)\left( {x - 3} \right) + 1} \right] > 0\) là

Câu 35:

Tập nghiệm của bất phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac+ % gacaGGNbWaaSbaaSqaamaalaaabaGaaGymaaqaaiaaikdaaaaabeaa % kmaalaaabaGaamiEaiabgUcaRiaaikdaaeaacaaIZaGaeyOeI0IaaG % OmaiaadIhaaaGaeyyzImRaaGimaaaa!430F! {\log _{\frac{1}{2}}}\frac{{x + 2}}{{3 - 2x}} \ge 0\) là

Câu 36:

Cho hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOzamaabm % aabaGaamiEaaGaayjkaiaawMcaaiabg2da9iGacYgacaGGVbGaai4z % amaaBaaaleaadaWcaaqaaiaaigdaaeaacaaIZaaaaaqabaGcdaqada % qaaiaadIhadaahaaWcbeqaaiaaikdaaaGccqGHsislcaaI1aGaamiE % aiabgUcaRiaaiEdaaiaawIcacaGLPaaaaaa!46BE! f\left( x \right) = {\log _{\frac{1}{3}}}\left( {{x^2} - 5x + 7} \right)\). Nghiệm của bất phương trình f(x) > 0 là:

Câu 37:

Bất phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac+ % gacaGGNbWaaSbaaSqaaiaaikdaaeqaaOGaamiEaiabgUcaRiGacYga % caGGVbGaai4zamaaBaaaleaacaaIZaaabeaakiaadIhacqGH+aGpca % aIXaaaaa!4217! {\log _2}x + {\log _3}x > 1\) có nghiệm là

Câu 38:

Bất phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac+ % gacaGGNbWaaSbaaSqaamaalaaabaGaaGymaaqaaiaaikdaaaaabeaa % kmaabmaabaGaciiBaiaac+gacaGGNbWaaSbaaSqaaiaaiodaaeqaaO % WaaSaaaeaacaaIYaGaamiEaiabgUcaRiaaigdaaeaacaWG4bGaeyOe % I0IaaGymaaaaaiaawIcacaGLPaaacqGH+aGpcaaIWaaaaa!479A! {\log _{\frac{1}{2}}}\left( {{{\log }_3}\frac{{2x + 1}}{{x - 1}}} \right) > 0\) có tập nghiệm là

Câu 39:

Tập nghiệm của bất phương trình: \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac+ % gacaGGNbWaaSbaaSqaamaalaaabaGaaGymaaqaaiaaiodaaaaabeaa % kmaabmaabaGaamiEaiabgkHiTiaaiodaaiaawIcacaGLPaaacqGHsi % slcaaIXaGaeyOpa4JaaGimaaaa!421C! {\log _{\frac{1}{3}}}\left( {x - 3} \right) - 1 > 0\) có dạng (a;b). Khi đó giá trị a + 3b bằng ?

Câu 40:

Tậpnghiệmcủabấtphươngtrình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac+ % gacaGGNbWaaSbaaSqaamaalaaabaGaaGymaaqaaiaaikdaaaaabeaa % kmaabmaabaGaciiBaiaac+gacaGGNbWaaSbaaSqaaiaaiAdaaeqaaO % WaaSaaaeaacaWG4bWaaWbaaSqabeaacaaIYaaaaOGaey4kaSIaamiE % aaqaaiaadIhacqGHRaWkcaaI0aaaaaGaayjkaiaawMcaaiabgYda8i % {\log _{\frac{1}{2}}}\left( {{{\log }_6}\frac{{{x^2} + x}}{{x + 4}}} \right) < 0\) là 

Câu 41:

Tập nghiệm của bất phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac+ % gacaGGNbWaaSbaaSqaaiaaiodaaeqaaOWaaeWaaeaaciGGSbGaai4B % aiaacEgadaWgaaWcbaWaaSaaaeaacaaIXaaabaGaaGOmaaaaaeqaaO % GaamiEaaGaayjkaiaawMcaaiabgYda8iaaigdaaaa!4289! {\log _3}\left( {{{\log }_{\frac{1}{2}}}x} \right) < 1\) là:

Câu 42:

Tìm tất cả giá trị thực của tham số m để bất phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac+ % gacaGGNbWaaSbaaSqaaiaaiodaaeqaaOWaaeWaaeaacaWG4bWaaWba % aSqabeaacaaIYaaaaOGaey4kaSIaaGinaiaadIhacqGHRaWkcaWGTb % aacaGLOaGaayzkaaGaeyyzImRaaGymaaaa!4421! {\log _3}\left( {{x^2} + 4x + m} \right) \ge 1\) nghiệm đúng với mọi ?

Câu 43:

Tìm tất cả các giá trị thực của tham số m để phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac+ % gacaGGNbWaaSbaaSqaaiaaikdaaeqaaOWaaeWaaeaacaWGTbGaamiE % aiabgkHiTiaadIhadaahaaWcbeqaaiaaikdaaaaakiaawIcacaGLPa % aacqGH9aqpcaaIYaaaaa!41CD! {\log _2}\left( {mx - {x^2}} \right) = 2\) vô nghiệm?

Câu 44:

Tìm tất cả các giá trị thực của tham số m để bất phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac+ % gacaGGNbWaaSbaaSqaaiaaikdaaeqaaOGaaiikaiaaiwdadaahaaWc % beqaaiaadIhaaaGccqGHsislcaaIXaGaaiykaiabgsMiJkaad2gaaa % a!4151! {\log _2}({5^x} - 1) \le m\) có nghiệm \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEaiabgw % MiZkaaigdaaaa!3972! x \ge 1\) ?

Câu 45:

Điều kiện xác định của bất phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaai4BaiaacE % gadaWgaaWcbaWaaSaaaeaacaaIXaaabaGaaGOmaaaaaeqaaOWaamWa % aeaaciGGSbGaai4BaiaacEgadaWgaaWcbaGaaGOmaaqabaGccaGGOa % GaaGOmaiabgkHiTiaadIhadaahaaWcbeqaaiaaikdaaaGccaGGPaaa % caGLBbGaayzxaaGaeyOpa4JaaGimaaaa!45F7! lo{g_{\frac{1}{2}}}\left[ {{{\log }_2}(2 - {x^2})} \right] > 0\) là:

Câu 46:

Điều kiện xác định của bất phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac6 % gadaWcaaqaaiaadIhadaahaaWcbeqaaiaaikdaaaGccqGHsislcaaI % XaaabaGaamiEaaaacqGH8aapcaaIWaaaaa!3E3B! \ln \frac{{{x^2} - 1}}{x} < 0\)

Câu 47:

Tìm số nghiệm nguyên của bất phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac+ % gacaGGNbWaaSbaaSqaamaakaaabaGaaG4maaadbeaaliabgkHiTiaa % igdaaeqaaOWaaeWaaeaacaWG4bWaaWbaaSqabeaacaaIYaaaaOGaey % OeI0IaaGOmaiaadIhacqGHRaWkcaaIXaaacaGLOaGaayzkaaGaeyOp % a4JaaGimaiaac6caaaa!45B6! {\log _{\sqrt 3 - 1}}\left( {{x^2} - 2x + 1} \right) > 0.\)

Câu 48:

Tập nghiệm của bất phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaai4BaiaacE % gadaWgaaWcbaGaaGOmaaqabaGccaGGOaGaamiEamaaCaaaleqabaGa % aGOmaaaakiabgkHiTiaaiodacaWG4bGaey4kaSIaaGymaiaacMcacq % GHKjYOcaaIWaaaaa!42C0! lo{g_2}({x^2} - 3x + 1) \le 0\) là ;

Câu 49:

Tập nghiệm của bất phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac+ % gacaGGNbWaaSbaaSqaamaalaaabaGaaGymaaqaaiaaikdaaaaabeaa % kmaabmaabaGaciiBaiaac+gacaGGNbWaaSbaaSqaaiaaikdaaeqaaO % WaaeWaaeaacaaIYaGaamiEaiabgkHiTiaaigdaaiaawIcacaGLPaaa % aiaawIcacaGLPaaacqGH+aGpcaaIWaaaaa!4678! {\log _{\frac{1}{2}}}\left( {{{\log }_2}\left( {2x - 1} \right)} \right) > 0\) là:

Câu 50:

Bất phương trình \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac+ % gacaGGNbWaaSbaaSqaamaalaaabaGaaGOmaaqaaiaaiodaaaaabeaa % kmaabmaabaGaaGOmaiaadIhadaahaaWcbeqaaiaaikdaaaGccqGHsi % slcaWG4bGaey4kaSIaaGymaaGaayjkaiaawMcaaiabgYda8iaaicda % aaa!43FC! {\log _{\frac{2}{3}}}\left( {2{x^2} - x + 1} \right) < 0\) có tập nghiệm là: