Trắc nghiệm Số phức Toán Lớp 12
-
Câu 1:
Gọi A là điểm biểu diễn của số phức z = 4 -7i và B là điểm biểu diễn của số phức z ' = -4+7i. Mệnh đề nào sau đây là đúng?
-
Câu 2:
Gọi A là điểm biểu diễn của số phức\(z=2+5 i\) và B là điểm biểu diễn của số phức \(z^{\prime}=-2+5 i\) . Mệnh đề nào sau đây là đúng?
-
Câu 3:
Gọi A là điểm biểu diễn của số phức \(z=-1+6 i\)và B là điểm biểu diễn của số phức \(z^{\prime}=-1-6 i\). Mệnh đề nào sau đây là đúng?
-
Câu 4:
Trong mặt phẳng tọa độ cho hai điểm A(4;0) và B(0;-3). Điểm C thỏa mãn điều kiện \(\overrightarrow{O C}=\overrightarrow{O A}+\overrightarrow{O B}\) . Khi đó, số phức được biểu diễn bởi điểm C là:
-
Câu 5:
Trong mặt phẳng tọa độ, điểm M là điểm biểu diễn của số phức z (như hình vẽ bên). Điểm nào trong hình vẽ là điểm biểu diễn của số phức 2z ?
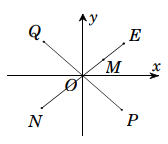
-
Câu 6:
Giả sử M, N, P, Q, đượccho ở hình vẽ bên là điểm biểu diễn của các số phức \(z_{1}, z_{2}, z_{3}, z_{4}\) trênmặt phẳng tọa độ. Khẳng định nào sau đây là đúng?
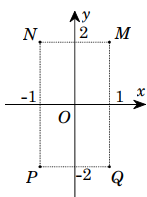
-
Câu 7:
Số phức nào dưới đây có điểm biểu diễn trên mặt phẳng tọa độ là điểm M như hình vẽ?
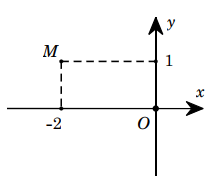
-
Câu 8:
Trong mặt phẳng tọa độ (hình vẽbên), số phức z=3-4i được biểu diễn bởi điểm nào trong các điểm A, B, C, D?
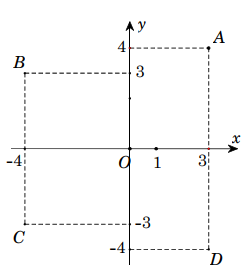
-
Câu 9:
Cho số phức \(z=1-2 i\) . Điểm nào dưới đây là điểm biểu diễn của số phức \(w=i z\) trên mặt phẳng tọa độ?
-
Câu 10:
Điểm biểu diễn số phức z=2-3i có tọa độ là:
-
Câu 11:
Với x y , là hai số thực thỏa mãn \(x(3+5 i)+y(1-2 i)^{3}=9+14 i\) . Tính giá trị của biểu thức \(P=2 x-3 y\)
-
Câu 12:
Cho số phức \(z=x+i y\text{ thỏa mãn }z^{2}=-8+6 i\) . Mệnh đề nào sau đây là sai?
-
Câu 13:
Cho hai số phức \(z_{1}=a+b i(a ; b \in \mathbb{R}) \text { và } z_{2}=3-4 i\). Biết \(z_{1}=z_{2}^{2}, \text { tính } P=a b\)
-
Câu 14:
Tìm tất cả các số thực x, y thỏa mãn \(x^{2}+y-(2 y+4) i=2 i\)
-
Câu 15:
Tìm tất cả các số thực x; y sao cho \(x^{2}-1+y i=-1+2 i\).
-
Câu 16:
Cho hai số thực x y , thỏa mãn \(2 x+3+(1-2 y) i=2(2-i)-3 y i+x\). Tính giá trị biểu thức \(P=x^{2}-3 x y-y\).
-
Câu 17:
Tìm tất cả các số thực x y ; thỏa mãn \((2 x-y) i+y(1-2 i)^{2}=3+7 i\)
-
Câu 18:
Biết rằng có duy nhất một cặp số thực (x;y) thỏa mãn \((x+y)+(x-y) i=5+3 i . \text { Tính } S=x+y\)
-
Câu 19:
Cho hai số phức \(z=(2 x+3)+(3 y-1) i\) và \(z^{\prime}=3 x+(y+1) i . \text { Khi } z=z^{\prime}\) , chọn khẳng định đúng trong các khẳng định sau:
-
Câu 20:
Cho hai số phức \(z_{1}=a+b i(a ; b \in \mathbb{R})\) và \(z_{2}=2017-2018 i\) . Biết \(z_{1}=z_{2}\) tính tổng S=a+2b
-
Câu 21:
Tập hợp các điểm trong mặt phẳng toạ độ biểu diễn các số phức z thoả mãn \(|z + 4 - 8i|= 2 \sqrt5\) là đường tròn có phương trình:
-
Câu 22:
Tập hợp các điểm biểu diễn cho số phức z thỏa mãn \(|z - 3 + 4i| = 5 \) là
-
Câu 23:
Trong mặt phẳng tọa độ, tập hợp điểm biểu diễn số phức z thỏa mãn \(|z - i| = |(1+ i ) z|\)là một đường tròn, đường tròn đó có phương trình là
-
Câu 24:
Trên mặt phẳng phức, tập hợp các điểm biểu diễn số phức z thỏa mãn \(|z + i| = |2\overline z - i|\)là một đường tròn có bán kính là R . Tính giá trị của R.
-
Câu 25:
Tập hợp điểm biểu diễn các số phức thỏa \(|zi +1 |= 1\)1 là một đường tròn. Tìm tâm I của đường tròn đó
-
Câu 26:
Tập hợp điểm biểu diễn các số phức z thỏa mãn \(|z - i |= |\overline z + 3|\)trong mặt phẳng Oxy là:
-
Câu 27:
Trong mặt phẳng phức, tập hợp các điểm biểu diễn của số phức z thỏa mãn điều
kiện \(|z + 2 | = |i - z|\) là đường thẳng \(\Delta\) có phương trình -
Câu 28:
Tìm tập hợp điểm biểu diễn của số phức z biết \(|z -1 |= |z + 2i |\)
-
Câu 29:
Trong mặt phẳng phức với hệ tọa độ Oxy , điểm biểu diễn của các số phức \(z = 3 + bi\, với\, b\in\mathbb{R}\) luôn nằm trên đường có phương trình là:
-
Câu 30:
Tập hợp điểm biểu diễn số phức z thỏa mãn \(|z|^2 = z^2\) là
-
Câu 31:
Tìm tập hợp những điểm M biểu diễn số phức z trong mặt phẳng phức, biết số phức z thỏa mãn điều kiện \(|z - 2i| = |\overline z +1 |\)
-
Câu 32:
Cho các số phức z thỏa mãn \(|z+1- i | = |z -1+ 2i |\). Tập hợp các điểm biểu diễn các số phức z trên mặt phẳng tọa độ là một đường thẳng. Phương trình đường thẳng đó là
-
Câu 33:
Trong mặt phẳng phức tập hợp điểm M ( z ) thoả mãn \({z_0}z + \overline {{z_0}z} + 1 = 0\,\,\rm{với }\,\,{z_0} = 1 - i\) là đường thẳng có phương trình
-
Câu 34:
Tập hợp các điểm trong mặt phẳng biểu diễn cho số phức z thoả mãn điều kiện \(z^2=(\overline z)^2\) là:
-
Câu 35:
Cho các số phức \(z_1 = -1+ i,z_2 = 2 + 3i,z_3 = 5 + i, z_4 = 2 - i \) lần lượt có các điểm biểu diễn trên mặt phẳng phức là M, N, P,Q . Hỏi tứ giác MNPQ là hình gì?
-
Câu 36:
Cho số phức \(z = m + (m - 3)i , m\in\mathbb{R}\) . Tìm m để điểm biểu diễn của số phức z nằm trên đường phân giác của góc phần tư thứ hai và thứ tư.
-
Câu 37:
Gọi M là điểm biểu diễn số phức \(z = i (1 + 2i )^2 \) . Tọa độ của điểm M là
-
Câu 38:
Cho số phức \(z = (1+ 2i)(2 - i) \), điểm biểu diễn của số phức i.z là
-
Câu 39:
Cho số phức z = 1 + 2i . Điểm nào dưới đây là điểm biểu diễn của số phức \( w = z + i\overline z\) trên mặt phẳng toạ độ?
-
Câu 40:
Giả sử A, B theo thứ tự là điểm biểu diễn của số phức \(z_1 , z_2\) . Khi đó độ dài của AB bằng
-
Câu 41:
Gọi A , B lần lượt là các điểm biểu diễn của các số phức \(z_1 = 1+ 2i ; z_2 = 5 - i \). Tính độ dài đoạn thẳng AB
-
Câu 42:
Điểm M trong hình vẽ bên là điểm biểu diễn số phức z tìm phần thực và phần ảo của số phức z
.png)
-
Câu 43:
Cho số phức z = 5 - 4i . Số phức đối của z có điểm biểu diễn là
-
Câu 44:
Điểm A trong hình vẽ bên biểu diễn cho số phức z
.png)
Tìm phần thực và phần ảo của số phức \(\overline z\)
-
Câu 45:
Cho số phức z thoả mãn \((2 + i) z = 10 - 5i\) . Hỏi điểm biểu diễn số phức z là điểm nào trong các điểm M,N, P, Q ở hình bên ?
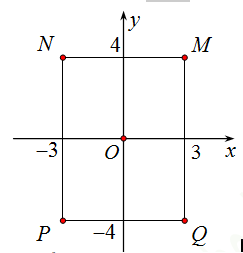
-
Câu 46:
Điểm M trong hình vẽ bên biểu diễn số phức \(\overline z\).
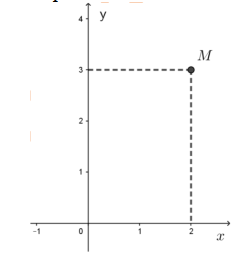
Số phức z bằng
-
Câu 47:
Trong hình vẽ bên, điểm M biểu diễn số phức z . Số phức \(\overline z\)
.png)
-
Câu 48:
Mệnh đề nào dưới đây sai?
-
Câu 49:
Phần thực của số phức \((1+ i)^{30} \) bằng
-
Câu 50:
Tìm phần ảo của số phức \(z = (1- i)^2 + (1+ i)^2\) .











