Cho hình chóp \(S.ABCD\) có đáy hình chữ nhật, tam giác \(SAB\) đều và nằm trong mặt phẳng vuông góc với đáy, \(AB = a;\,\,AD = a\sqrt 3 \). Thể tích khối chóp S.ABCD bằng?
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiPhương pháp:
- Gọi \(H\) là trung điểm của AB, chứng minh \(SH \bot \left( {ABCD} \right)\).
- Tính thể tích khối chóp \({V_{S.ABCD}} = \dfrac{1}{3}SH.{S_{ABCD}}\).
Cách giải:
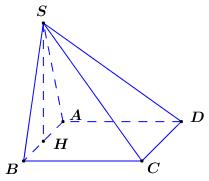
Gọi \(H\) là trung điểm của AB, vì \(\Delta SAB\) đều có \(AB = a\) nên \(SH \bot AB\) và \(SH = \dfrac{{a\sqrt 3 }}{2}\).
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{\left( {SAB} \right) \bot \left( {ABCD} \right) = AB}\\{SH \subset \left( {SAB} \right);{\mkern 1mu} {\mkern 1mu} SH \bot AB}\end{array}} \right.\) \( \Rightarrow SH \bot \left( {ABCD} \right)\).
Ta có: \({S_{ABCD}} = AB.AD = a.a\sqrt 3 {\rm{\;}} = {a^2}\sqrt 3 \).
Vậy \({V_{S.ABCD}} = \dfrac{1}{3}SH.{S_{ABCD}} = \dfrac{1}{3}.\dfrac{{a\sqrt 3 }}{2}.{a^2}\sqrt 3 {\rm{\;}} = \dfrac{{{a^3}}}{2}\).
Chọn D.
Đề thi giữa HK2 môn Toán 12 năm 2023-2024
Trường THPT Lạc Long Quân