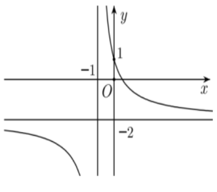
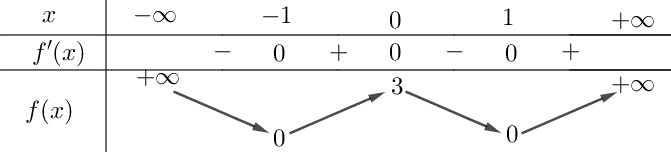Cho hàm số bậc bốn \(y=f\left( x \right)=a{{x}^{4}}+b{{x}^{3}}+c{{x}^{2}}+dx+e\) thỏa mãn \(f\left( 0 \right)=3f\left( 2 \right)=-3\) và có đồ thị hàm số \(y={f}'\left( x \right)\) như hình bên dưới.
Có bao nhiêu giá trị nguyên của tham số \(m\) thuộc khoảng \(\left( -20;20 \right)\) để hàm số \(g\left( x \right)=f\left[ 4f\left( x \right)-f''\left( x \right)+m \right]\) đồng biến trên khoảng \(\left( 0;1 \right)?\)
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiXét \(y=f\left( x \right)=a{{x}^{4}}+b{{x}^{3}}+c{{x}^{2}}+dx+e\Rightarrow f'\left( x \right)=4a{{x}^{3}}+3b{{x}^{2}}+2cx+d\).
Từ đồ thị \(y={f}'\left( x \right)\) ta có \({f}'(x)=4ax\left( {{x}^{2}}-1 \right)=4a{{x}^{3}}-4ax.\)
Vậy ta có hệ phương trình
\(\begin{array}{l} \left\{ \begin{array}{l} b = 0\\ 2c = - 4\\ d = 0 \end{array} \right.a\\ \Leftrightarrow \left\{ \begin{array}{l} b = 0\\ c = - 2a\\ d = 0 \end{array} \right. \end{array}\)
\(\Rightarrow f\left( x \right)=a{{x}^{4}}-2a{{x}^{2}}+e\).
Ta lại có
\(f\left( 0 \right)=3f\left( 2 \right)=-3\\\Rightarrow \left\{ \begin{align} & a=\frac{1}{4} \\ & e=-3 \\ \end{align} \right.\)
Vậy \(f\left( x \right)=\frac{1}{4}{{x}^{4}}-\frac{1}{2}{{x}^{2}}-3.\)
Ta có \({f}'(x)={{x}^{3}}-x\)\(\Rightarrow f''\left( x \right)=3{{x}^{2}}-1\)\(\Rightarrow f'''\left( x \right)=6x\)
Xét hàm số \(g\left( x \right)=f\left( 2f\left( x \right)-f''\left( x \right)+m \right)\) trên đoạn \(\left[ 0;1 \right]\)
Ta có \(g'\left( x \right)=\left[ 4f'\left( x \right)-f'''\left( x \right) \right]f'\left[ 4f\left( x \right)-f''\left( x \right)+m \right]\)
Hàm số \(g\left( x \right)\) đồng biến trên khoảng \(\left( 0;1 \right)\) \(\Leftrightarrow g'\left( x \right)\ge 0,\forall x\in \left( 0;1 \right).\)
Mà \(4f'\left( x \right)-f'''\left( x \right)<0,\forall x\in \left( 0;1 \right)\) và \(4f\left( x \right)-f''\left( x \right)+m={{x}^{4}}-5{{x}^{2}}+m-11\)
Nên \(g'\left( x \right)\ge 0,\forall x\in \left( 0;1 \right)\)
\(\Leftrightarrow f'\left[ 4f\left( x \right)-f''\left( x \right)+m \right]\le 0,\forall x\in \left( 0;1 \right)\Leftrightarrow f'\left( {{x}^{4}}-5{{x}^{2}}+m-11 \right)\le 0,\forall x\in \left( 0;1 \right)\)
\(\begin{array}{l} \Leftrightarrow \left[ \begin{array}{l} {x^4} - 5{x^2} + m - 11 \le - 1,\forall x \in \left( {0;1} \right)\\ 0 \le {x^4} - 5{x^2} + m - 11 \le 1,\forall x \in \left( {0;1} \right) \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l} m - 10 \le - {x^4} + 5{x^2},\forall x \in \left( {0;1} \right)\\ \left\{ \begin{array}{l} m - 11 \ge - {x^4} + 5{x^2},\forall x \in \left( {0;1} \right)\\ m - 12 \le - {x^4} + 5{x^2},\forall x \in \left( {0;1} \right) \end{array} \right. \end{array} \right.\quad \left( * \right) \end{array}\)
Xét hàm số \(h\left( x \right)=-{{x}^{4}}+5{{x}^{2}}\) trên \(\left[ 0;1 \right]\)
Tìm được \(\underset{\left[ 0;1 \right]}{\mathop{\min }}\,h\left( x \right)=0,\)\(\underset{\left[ 0;1 \right]}{\mathop{\max }}\,h\left( x \right)=4.\)
Do đó
\(\begin{array}{l} \left( * \right) \Leftrightarrow \left[ \begin{array}{l} m - 10 \le 0\\ \left\{ \begin{array}{l} m - 11 \ge 4\\ m - 12 \le 0 \end{array} \right. \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l} m \le 10\\ \left\{ \begin{array}{l} m \ge 15\\ m \le 12 \end{array} \right. \end{array} \right. \Leftrightarrow m \le 10. \end{array}\)
\(m\) nguyên thuộc khoảng \(\left( -20;20 \right)\Rightarrow m\in \left\{ -19,...,10 \right\}\)
\(\Rightarrow \) có 30 giá trị nguyên của m.
Đề thi thử tốt nghiệp THPT môn Toán năm 2023
Trường THPT Vụ Bản
.PNG)
.PNG)
.PNG)