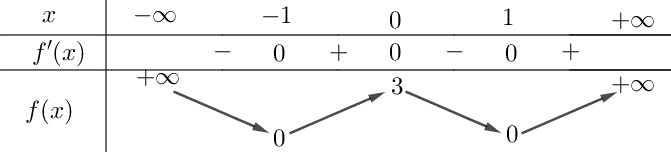Xét các số thực \(x,y\)thỏa mãn \({{2}^{{{x}^{2}}+{{y}^{2}}+1}}\le \left( {{x}^{2}}+{{y}^{2}}-2x+2 \right){{.4}^{x}}\). Giá trị lớn nhất của biểu thức \(P=\frac{8x+4}{2x-y+1}\) gần nhất với số nào dưới đây
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiChọn C
Nhận xét \({{x}^{2}}+{{y}^{2}}-2x+2>0\forall x;y\)
Bất phương trình \({{2}^{{{x}^{2}}+{{y}^{2}}+1}}\le \left( {{x}^{2}}+{{y}^{2}}-2x+2 \right){{.4}^{x}}\)\(\Leftrightarrow \frac{{{2}^{{{x}^{2}}+{{y}^{2}}+1}}}{{{2}^{2x}}}\le \left( {{x}^{2}}+{{y}^{2}}-2x+2 \right)\)\(\Leftrightarrow {{2}^{{{x}^{2}}+{{y}^{2}}-2x+1}}\le \left( {{x}^{2}}+{{y}^{2}}-2x+2 \right)\).
Đặt \(t={{x}^{2}}+{{y}^{2}}-2x+1\)
Bất phương trình\(\Leftrightarrow {{2}^{t}}\le t+1\)\(\Leftrightarrow {{2}^{t}}-t-1\le 0\)
Đặt \(f\left( t \right)={{2}^{t}}-t-1\). Ta thấy \(f\left( 0 \right)=f\left( 1 \right)=0\).
Ta có \({f}'\left( t \right)={{2}^{t}}\ln 2-1\)
\({f}'\left( t \right)=0\Leftrightarrow {{2}^{t}}\ln 2=1\Leftrightarrow t={{\log }_{2}}\left( \frac{1}{\ln 2} \right)\approx 0,52\)
.PNG)
Quan sát BBT ta thấy \(f\left( t \right)\le 0\Leftrightarrow 0\le t\le 1\)
\(\Rightarrow 0\le {{x}^{2}}+{{y}^{2}}-2x+1\le 1\)\(\Leftrightarrow {{\left( x-1 \right)}^{2}}+{{y}^{2}}\le 1\) \(\left( 1 \right)\)
Khi đó tập hợp các điểm \(M\left( x;y \right)\) là một hình tròn \(\left( S \right)\) tâm \(I\left( 1;0 \right)\), bán kính \(R=1\).
Xét \(P=\frac{8x+4}{2x-y+1}\Leftrightarrow \left( 2P-8 \right)x-Py+P-4=0\)
Khi đó ta cũng có tập hợp các điểm \(M\left( x;y \right)\) là một đường thẳng \(\Delta :\left( 2P-8 \right)x-Py+P-4=0\).
Để \(\Delta \) và \(\left( S \right)\) có điểm chung, ta suy ra \(d\left( I,\Delta \right)\le 1\).
\(\Leftrightarrow \frac{\left| 2P-8+P-4 \right|}{\sqrt{{{\left( 2P-8 \right)}^{2}}+{{P}^{2}}}}\le 1\Leftrightarrow \left| 3P-12 \right|\le \sqrt{5{{P}^{2}}-32P+64}\)
\(\Leftrightarrow 4{{P}^{2}}-40P+80\le 0\)\(\Leftrightarrow 5-\sqrt{5}\le P\le 5+\sqrt{5}\).
Vậy giá trị nhỏ nhất của \(P\)là \(5+\sqrt{5}\approx 7,23\) khi
\(\left\{ \begin{align} & x=\frac{1}{3} \\ & y=\frac{\sqrt{5}}{3} \\ \end{align} \right.\)
Đề thi thử tốt nghiệp THPT môn Toán năm 2023
Trường THPT Vụ Bản
Câu hỏi liên quan
-
Giá trị nhỏ nhất của hàm số \(f\left( x \right)={{x}^{3}}-6x\) trên đoạn \(\left[ -1;4 \right]\) là
-
Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như sau
Tiệm cận ngang của đồ thị hàm số là
-
Cho hình phẳng giới hạn bởi đồ thị hàm số \(y=\sin x\), trục \(Ox\) và các đường thẳng \(x=0,x=\pi \)quay xung quanh \(Ox.\) Thể tích khối tròn xoay tạo thành bằng
-
Trong các khẳng định sau, khẳng định nào sai?
-
Cho hàm số \(f\left( x \right)\) biết hàm số \(y={{f}'}'(x)\) là hàm đa thức bậc bốn có đồ thị như hình vẽ bên.
.PNG)
Đặt \(g(x)=2f\left( \frac{1}{2}{{x}^{2}} \right)+f\left( -{{x}^{2}}+6 \right)\), biết rằng \(g(0)>0\) và \(g\left( 2 \right)<0.\) Số điểm cực tiểu của hàm số \(y=\left| g\left( x \right) \right|\) là
-
Năm \(2023\) một hãng xe niêm yết giá bán loại xe X là \(750.000.000\) đồng và dự định trong \(10\) năm tiếp theo, mỗi năm giảm \(2%\) giá bán so với giá bán của năm liền trước. Theo dự định đó, năm \(2030\) hãng xe ô tô niêm yết giá bán loại xe X là bao nhiêu? (kết quả làm tròn đến hàng nghìn)
-
Cho hình chóp \(S.ABC\) có \(SA\) vuông góc với đáy, tam giác \(ABC\) có \(AB=a,\)\(AC=2a,\widehat{\,BAC}=120{}^\circ \) (tham khảo hình vẽ). Khoảng cách từ điểm \(B\) đến mặt phẳng \(\left( SAC \right)\) bằng
.PNG)
-
Cho hàm số \(y=f\left( x \right)=a{{x}^{4}}+b{{x}^{2}}+c\) có đồ thị như hình vẽ bên. Số giá trị nguyên dương của tham số \(m\) để phương trình \(f\left( x \right)=m\) có hai nghiệm phân biệt là
-
Trong không gian \(Oxyz,\) cho mặt cầu \(\left( S \right):{{x}^{2}}+{{y}^{2}}+{{\left( z-3 \right)}^{2}}=8\) và hai điểm \(A\left( 4;-4;3 \right),\)\)B\left( 1;-1;7 \right).\) Gọi \(\left( {{C}_{1}} \right)\) là tập hợp các điểm \(M\in (S)\) sao cho biểu thức \(\left| MA-2MB \right|\) đạt giá trị nhỏ nhất. Biết \(\left( {{C}_{1}} \right)\) là một đường tròn, bán kính của đường tròn đó là
-
Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau
.PNG)
Giá trị cực tiểu của hàm số \(y=f\left( x \right)+1\) bằng
-
Trong không gian \(Oxyz,\) cho hai điểm \(A\left( 1;-2;5 \right)\) và \(B\left( -2;-2;1 \right).\) Độ dài đoạn thẳng \(AB\) bằng
-
Cho khối lăng trụ tam giác có chiều cao \(h=3\) và đáy là tam giác đều cạnh \(a=2.\) Thể tích khối lăng trụ đã cho bằng
-
Nghiệm của phương trình \({{2}^{1-3x}}=\frac{1}{32}\) là
-
Cho hàm số bậc bốn \(f\left( x \right)=a{{x}^{4}}+b{{x}^{3}}+c{{x}^{2}}+dx+e\ \left( a,b,c,d,e\in \mathbb{R} \right)\) và hàm số bậc ba \(g\left( x \right)=m{{x}^{3}}+n{{x}^{2}}+px+q\ \left( m,n,p,q\in \mathbb{R} \right)\) có đồ thị \(y=f'\left( x \right)\) và \(y=g'\left( x \right)\) như hình vẽ bên dưới.
.PNG)
Biết diện tích hình phẳng giới hạn bởi hai đồ thị hàm số \(y=f\left( x \right)\) và \(y=g\left( x \right)\) bằng 96 và \(f\left( 2 \right)=g\left( 2 \right)\). Diện tích hình phẳng giới hạn bởi các đường \(y=f\left( x \right),y=g\left( x \right)\) và \(x=0,\ x=2\) bằng
-
Một họa sĩ cần trưng bày \(10\) bức tranh nghệ thuật khác nhau thành một hàng ngang. Hỏi có bao nhiêu cách để họa sĩ sắp xếp các bức tranh?
-
Cho hình trụ có bán kính đáy \(r=3\) và độ dài đường sinh \(l=5.\) Diện tích xung quanh của hình trụ đã cho bằng
-
Trong không gian \(Oxyz,\) cho hai điểm \(A\left( -10;6;-2 \right),B\left( -5;10;-9 \right)\) và mặt phẳng \(\left( \alpha \right):2x-2y-z+12=0\). Điểm \(M\left( a;b;c \right)\) thuộc \(\left( \alpha \right)\) sao cho \(MA,MB\) tạo với \(\left( \alpha \right)\) các góc bằng nhau và biểu thức \(T=2M{{A}^{2}}-M{{B}^{2}}\) đạt giá trị nhỏ nhất. Tổng \(a+b+c\) bằng
-
Hàm số nào dưới đây có bảng biến thiên như hình sau
-
Với \(a,b\) là các số thực dương tùy ý thỏa mãn \({{\log }_{3}}b-2{{\log }_{9}}a=2.\)Mệnh đề nào dưới đây đúng?
-
Gọi \(S\) là tập hợp tất cả các số tự nhiên có ít nhất 3 chữ số và các chữ số đôi một khác nhau được lập từ các chữ số \(1,2,3,4,5.\)Chọn ngẫu nhiên hai số từ \(S,\) tính xác xuất để hai số chọn được đều là số có ba chữ số.
