Cho hàm số \(f\left( x \right)\) biết hàm số \(y={{f}'}'(x)\) là hàm đa thức bậc bốn có đồ thị như hình vẽ bên.
Đặt \(g(x)=2f\left( \frac{1}{2}{{x}^{2}} \right)+f\left( -{{x}^{2}}+6 \right)\), biết rằng \(g(0)>0\) và \(g\left( 2 \right)<0.\) Số điểm cực tiểu của hàm số \(y=\left| g\left( x \right) \right|\) là
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTừ đồ thị hàm số \(y={{f}'}'(x)\) ta có \({{f}'}'(x)>0\,,\forall x\in \mathbb{R}\)\(\Rightarrow \) Hàm số \(y={f}'\left( x \right)\) đồng biến trên \(\mathbb{R}\).
\({g}'(x)=2x.{f}'\left( \frac{1}{2}{{x}^{2}} \right)-2x.{f}'\left( -{{x}^{2}}+6 \right)=2x\left[ {f}'\left( \frac{1}{2}{{x}^{2}} \right)-{f}'\left( -{{x}^{2}}+6 \right) \right]\).
\(\begin{array}{l} g'(x) = 0\\ \Leftrightarrow \left[ \begin{array}{l} 2x = 0\\ f'\left( {\frac{1}{2}{x^2}} \right) = f'\left( { - {x^2} + 6} \right) \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l} x = 0\\ \frac{1}{2}{x^2} = - {x^2} + 6 \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l} x = 0\\ x = - 2\\ x = 2 \end{array} \right. \end{array}\)
( do hàm số \(y={f}'\left( x \right)\) đồng biến trên \(\mathbb{R}\))
Xét \(g'(x)>0\Leftrightarrow \) \(2x\left[ {f}'\left( \frac{1}{2}{{x}^{2}} \right)-{f}'\left( -{{x}^{2}}+6 \right) \right]>0\).
\(\begin{array}{l} \Leftrightarrow \left[ \begin{array}{l} \left\{ \begin{array}{l} x > 0\\ \frac{1}{2}{x^2} > - {x^2} + 6 \end{array} \right.\\ \left\{ \begin{array}{l} x < 0\\ \frac{1}{2}{x^2} < - {x^2} + 6 \end{array} \right. \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l} x > 2\\ - 2 < x < 0 \end{array} \right. \end{array}\)
Suy ra \({g}'(x)<0\)
\({g}'(x)<0\Leftrightarrow \left[ \begin{align}
& x<-2 \\
& 0 < x < 2 \\
\end{align} \right.\)
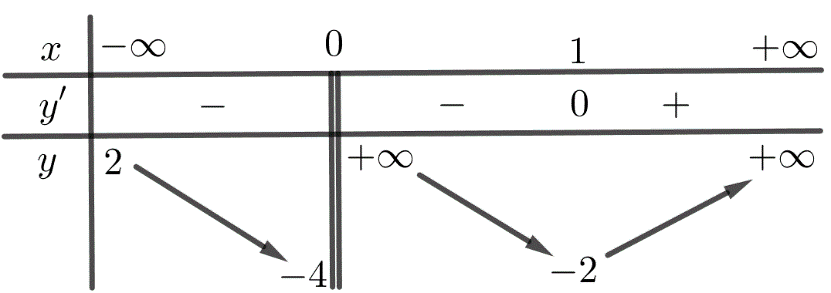
Vì \(g(x)=2f\left( \frac{1}{2}{{x}^{2}} \right)+f\left( -{{x}^{2}}+6 \right)\) là hàm số chẵn trên \(\mathbb{R}\) và có \(g\left( 2 \right)<0\) nên \(g\left( -2 \right)=g\left( 2 \right)=a<0,\,\,g(0)=b>0\).
Bảng biến thiên của hàm số \(g\left( x \right)\):
Vậy hàm số \(y=\left| g(x) \right|\) có 4 điểm cực tiểu. Chọn B.
Đề thi thử tốt nghiệp THPT môn Toán năm 2023
Trường THPT Vụ Bản
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
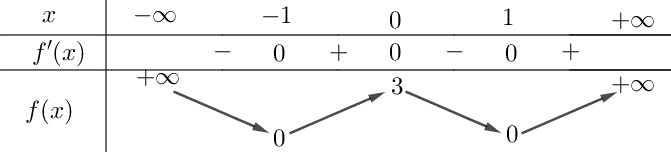
.PNG)
.PNG)











