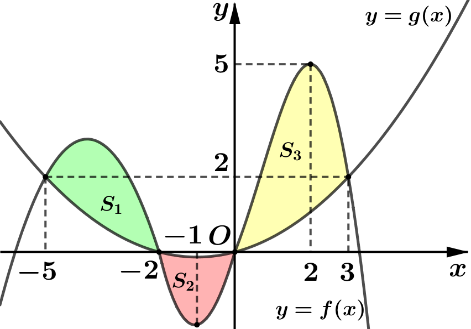
Cho hàm số \(y=f\left( x \right)\) xác định và liên tục trên đoạn \(\left[ -5;\,3 \right]\) và có đồ thị như hình vẽ. Biết rằng diện tích hình phẳng \({{S}_{1}},\,\,{{S}_{2}},\,\,{{S}_{3}}\) giới hạn bởi đồ thị hàm số \(y=f\left( x \right)\) và đường cong \(y=g\left( x \right)=a{{x}^{2}}+bx+c\) lần lượt là \(m,\,\,n,\,\,p.\)

Tích phân \(\int\limits_{-5}^{3}{f\left( x \right)\text{d}x}\) bằng

Câu hỏi liên quan

• Có bao nhiêu số nguyên \(x\) thỏa mãn \(\text{lo}{{\text{g}}_{3}}\frac{{{x}^{2}}-9}{125}\le \text{lo}{{\text{g}}_{5}}\frac{{{x}^{2}}-9}{27}\)?

• Cho khối trụ \(\left( T \right)\) có bán kính đáy bằng \(2\) và chiều cao bằng \(4\). Thể tích khối trụ \(\left( T \right)\) bằng

• Cho \(M\) là giao điểm của đồ thị hàm số \(y=\frac{x+1}{x-2}\) với trục hoành. Phương trình tiếp tuyến với đồ thị hàm số trên tại điểm \(M\) là

ZUNIA12

• Cho hình phẳng \(\left( H \right)\) giới hạn bởi đồ thị \(\left( P \right):y=2x-{{x}^{2}}\) và trục \(Ox\). Tính thể tích của khối tròn xoay tạo thành khi cho \(\left( H \right)\) quay quanh trục \(Ox\).

• Tập nghiệm của bất phương trình \({{\log }_{2}}\left( x-2 \right)<1\) là

• Số nghiệm nguyên của bất phương trình \({{\log }_{\frac{1}{4}}}\left( x-1 \right)+{{\log }_{4}}\left( 14-2x \right)\ge 0\)

• Cho đồ thị hàm số \(y=\frac{x}{x-2}\). Khẳng định nào sau đây đúng?

• Số điểm cực trị của hàm số \(y=-{{x}^{4}}-4{{x}^{3}}+3\) là

• Với \(a,b\) là các số thực dương bất kì, \({{\log }_{2}}\left( a{{b}^{3}} \right)\) bằng:

• Trong các hàm số sau đây, hàm số nào là nguyên hàm của hàm số \(f\left( x \right)=\frac{1}{x-3}\)?

• Cho hình nón có diện tích xung quanh bằng \(8\pi \) và độ dài đường sinh là \(4\). Tính bán kính đường tròn đáy của hình nón.

• Trong không gian với hệ tọa độ \(Oxyz\), vectơ \(\overrightarrow{a}=\left( 1;2;-2 \right)\) vuông góc với vectơ nào sau đây?

• Cho hàm số \(y=f\left( x \right)\) xác định và liên tục trên đoạn \(\left[ a;\,b \right]\). Diện tích \(S\)của hình phẳng được giới hạn bởi đồ thị hàm số \(y=f\left( x \right)\), trục hoành, đường thẳng \(x=a,x=b\)được tính theo công thức

• Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật, \(AD=2\sqrt{2},\,\,AB=1,\,\,\)

  \(SA=SB,\,\)\(SC=SD.\) Biết rằng hai mặt phẳng \(\left( SAB \right)\) và \(\left( SCD \right)\) vuông góc với nhau và tổng diện tích của hai tam giác \(SAB\) và \(SCD\) bằng \(\sqrt{3}.\) thể tích của khối chóp \(S.ABCD\) bằng

• Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như sau

  

  Hàm số đã cho đồng biến trên khoảng nào dưới đây?

• Có bao nhiêu giá trị nguyên của tham số \(m\) để hàm số \(y=\frac{1}{3}{{x}^{3}}-{{x}^{2}}-mx+2023\) có hai điểm cực trị thuộc khoảng \(\left( -4;3 \right)\)?

• Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh \(a,\,\,SA\bot \left( ABC \right)\) và góc giữa đường thẳng \(SB\) và mặt phẳng \(\left( ABC \right)\) bằng \({{60}^{0}}\). Thể tích khối chóp \(S.ABC\) bằng

• Trong không gian \(Oxyz,\) cho mặt phẳng \(\left( P \right):x-y+z+7=0,\) đường thẳng \(d:\frac{x}{1}=\frac{y}{-2}=\frac{z}{2}\) và mặt cầu \(\left( S \right):{{\left( x-1 \right)}^{2}}+{{y}^{2}}+{{\left( z-2 \right)}^{2}}=5.\) Gọi \(A,\,\,B\) là hai điểm trên mặt cầu \(\left( S \right)\) và \(AB=4;\) \({A}',\,\,{B}'\) là hai điểm nằm trên mặt phẳng \(\left( P \right)\) sao cho \(A{A}',\,\,B{B}'\) cùng song song với đường thẳng \(d.\) Giá trị lớn nhất của tổng \(A{A}'+\,B{B}'\) gần nhất với giá trị nào sau đây

• Nghiệm của phương trình \({{2023}^{x-1}}=1\) là

• Cho hình lăng trụ tam giác đều \(ABC.{A}'{B}'{C}'\) có cạnh đáy bằng \(a\) cạnh bên bằng \(\frac{3a}{2}\). Góc giữa hai mặt phẳng \(\left( {A}'BC \right)\)và mặt phẳng \(\left( ABC \right)\)bằng