Cho lăng trụ đều \(ABC.{A}'{B}'{C}'\) có cạnh đáy bằng \(a\), góc giữa đường thẳng \(A{B}'\) và mặt phẳng \((BC{B}'{C}')\) bằng \({{30}^{0}}\). Tính thể tích khối lăng trụ \(ABC.{A}'{B}'{C}'\).

Câu hỏi liên quan

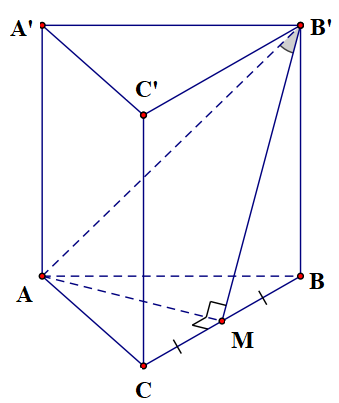
• Cho hình chóp \(S.ABC\) có \({A}',\,\,{B}'\) lần lượt là trung điểm của \(SA,\,\,SB\). Mặt phẳng \(\left( C{A}'{B}' \right)\) chia khối chóp thành hai khối đa diện có thể tích lần lượt là \({{V}_{1}},\,\,{{V}_{2}}\) \(\left( {{V}_{1}}>{{V}_{2}} \right)\). Tỉ số \(\frac{{{V}_{1}}}{{{V}_{2}}}\) gần với số nào nhất?

  

• Tổng hai nghiệm của phương trình \({{2}^{{{x}^{2}}+x+1}}={{8}^{2x}}\)

• Thể tích khối cầu nội tiếp hình lập phương cạnh \(2a\) là

ZUNIA12

• Trong không gian với hệ tọa độ \(Oxyz\), cho đường thẳng \(\Delta :\frac{x-2}{1}=\frac{y+2}{2}=\frac{z}{-2}\) và mặt phẳng \(\left( P \right):2x-y+2z-2022=0\). Gọi \(\alpha \) là góc giữa đường thẳng \(\Delta \) và mặt phẳng \(\left( P \right)\). Khẳng định nào sau đây đúng ?

• Cho khối trụ \(\left( T \right)\) có bán kính đáy bằng \(2\) và chiều cao bằng \(4\). Thể tích khối trụ \(\left( T \right)\) bằng

• Trong không gian \(Oxyz,\) cho mặt phẳng \(\left( P \right):x-y+z+7=0,\) đường thẳng \(d:\frac{x}{1}=\frac{y}{-2}=\frac{z}{2}\) và mặt cầu \(\left( S \right):{{\left( x-1 \right)}^{2}}+{{y}^{2}}+{{\left( z-2 \right)}^{2}}=5.\) Gọi \(A,\,\,B\) là hai điểm trên mặt cầu \(\left( S \right)\) và \(AB=4;\) \({A}',\,\,{B}'\) là hai điểm nằm trên mặt phẳng \(\left( P \right)\) sao cho \(A{A}',\,\,B{B}'\) cùng song song với đường thẳng \(d.\) Giá trị lớn nhất của tổng \(A{A}'+\,B{B}'\) gần nhất với giá trị nào sau đây

• Số điểm cực trị của hàm số \(y=-{{x}^{4}}-4{{x}^{3}}+3\) là

• Tìm \(a\) để đồ thị hàm số \(y={{\log }_{a}}x\left( 0<a\ne 1 \right)\) có đồ thị là hình bên.

  

• Có bao nhiêu số nguyên \(x\) thỏa mãn \(\text{lo}{{\text{g}}_{3}}\frac{{{x}^{2}}-9}{125}\le \text{lo}{{\text{g}}_{5}}\frac{{{x}^{2}}-9}{27}\)?

• Cho \(M\) là giao điểm của đồ thị hàm số \(y=\frac{x+1}{x-2}\) với trục hoành. Phương trình tiếp tuyến với đồ thị hàm số trên tại điểm \(M\) là

• Trên tập hợp các số phức, xét phương trình \({{z}^{2}}-2\left( m+1 \right)z+{{m}^{2}}=0\) (\(m\) là tham số thực). Có bao nhiêu giá trị của \(m\) để phương trình đó có nghiệm \({{z}_{0}}\) thỏa mãn \(\left| {{z}_{0}} \right|=7?\)

• Đồ thị hàm số nào dưới đây có dạng của hình bên?

  

• Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như sau

  

  Hàm số đã cho đồng biến trên khoảng nào dưới đây?

• Cấp số nhân \(\left( {{u}_{n}} \right)\) có số hạng đầu \({{u}_{1}}=1\), công bội \(q=2\), số hạng thứ tư là

• Cho số phức \(z=1+i\). Môđun của số phức \(w=\left( 1+3i \right)z\) là

• Cho hình phẳng \(\left( H \right)\) giới hạn bởi đồ thị \(\left( P \right):y=2x-{{x}^{2}}\) và trục \(Ox\). Tính thể tích của khối tròn xoay tạo thành khi cho \(\left( H \right)\) quay quanh trục \(Ox\).

• Cho hàm số \(f\left( x \right)={{x}^{4}}+b{{x}^{2}}+c\left( b,c\in \mathbb{R} \right)\) có đồ thị là đường cong \(\left( C \right)\) và đường thẳng \(\left( d \right):y=g\left( x \right)\) tiếp xúc với \(\left( C \right)\) tại điểm \({{x}_{0}}=1\). Biết \(\left( d \right)\) và \(\left( C \right)\) còn hai điểm chung khác có hoành độ là \({{x}_{1}},{{x}_{2}}\left( {{x}_{1}}<{{x}_{2}} \right)\) và \(\int\limits_{{{x}_{1}}}^{{{x}_{2}}}{\frac{g\left( x \right)-f\left( x \right)}{{{\left( x-1 \right)}^{2}}}dx=\frac{4}{3}}\). Tính diện tích hình phẳng giới hạn bởi đường cong \(\left( C \right)\) và đường thẳng \(\left( d \right)\).

   

• Trong không gian với hệ tọa độ \(Oxyz\), điểm \(M'\)đối xứng với điểm \(M\left( 2;\,2;\,-1 \right)\)qua mặt phẳng \(\left( Oyz \right)\) có tọa độ là

• Có bao nhiêu giá trị nguyên của tham số \(m\) để hàm số \(y=\frac{1}{3}{{x}^{3}}-{{x}^{2}}-mx+2023\) có hai điểm cực trị thuộc khoảng \(\left( -4;3 \right)\)?

• Trong không gian với hệ tọa độ \(Oxyz\), vectơ \(\overrightarrow{a}=\left( 1;2;-2 \right)\) vuông góc với vectơ nào sau đây?