Cho \(g\left( x \right)={{x}^{2}}-2x-1\) và hàm số \(y=f\left( x \right)\) có bảng biến thiên như hình vẽ:
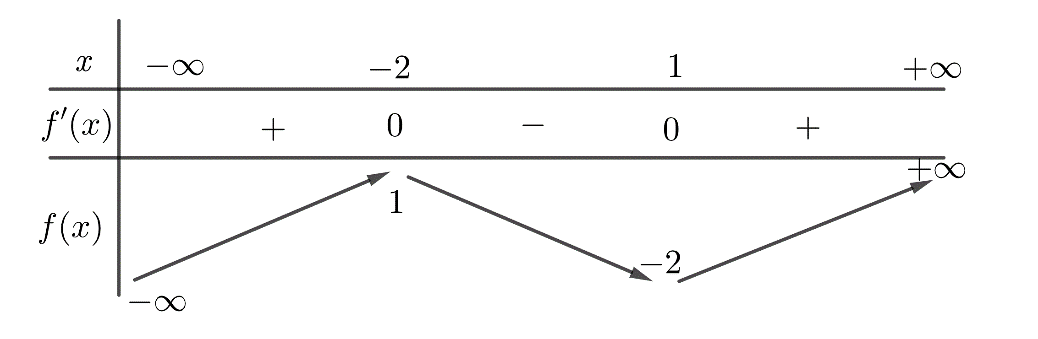
Số nghiệm của phương trình \(f\left[ g\left( x \right) \right]=0\) là
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiChọn B
Dựa trên BBT:
\(f(x)=0\Leftrightarrow \left[ \begin{matrix} x=a\in (-\infty ;-2) \\ x=b\in (-2;1) \\ x=c\in (1;+\infty ) \\ \end{matrix} \right.\)
\(f\left[ g\left( x \right) \right]=0\)
\(\Leftrightarrow \left[ \begin{matrix} g(x)=a\in (-\infty ;-2) \\ g(x)=b\in (-2;1) \\ g(x)=c\in (1;+\infty ) \\ \end{matrix} \right.\)
Xét \(g\left( x \right)={{x}^{2}}-2x-1\), ta có
\({g}'\left( x \right)=2x-2=0\Leftrightarrow x=1\Rightarrow g\left( 1 \right)=-2\)
BBT
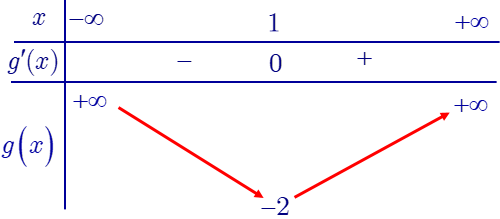
Dựa vào BBT của \(g\left( x \right)={{x}^{2}}-2x-1\) ta có:
\(g\left( x \right)=a\in (-\infty ;-2)\) phương trình vô nghiệm.
\(g\left( x \right)=b\) (với \(b\in (-2;1)\)) có 2 nghiệm phân biệt
\(g\left( x \right)=c\) (với \(c\in (1;+\infty )\)) có 2 nghiệm phân biệt
Vậy \(f\left[ g\left( x \right) \right]=0\) có 4 nghiệm phân biệt.
Đề thi thử tốt nghiệp THPT môn Toán năm 2023
Trường THPT Gia Định
.png)