Có bao nhiêu giá trị nguyên của tham số \(m\) để hàm số \(y=\frac{1}{3}{{x}^{3}}-{{x}^{2}}-mx+2023\) có hai điểm cực trị thuộc khoảng \(\left( -4;3 \right)\)?
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiChọn C
Ta có: \(y'={{x}^{2}}-2x-m\). Xét phương trình \(y'=0\Leftrightarrow {{x}^{2}}-2x-m=0\,\,\,\,\,\left( 1 \right)\).
Để hàm số có hai điểm cực trị thuộc khoảng \(\left( -4;3 \right)\) thì phương trình \(\left( 1 \right)\) phải có 2 nghiệm phân biệt thuộc khoảng \(\left( -4;3 \right)\)
Ta có: \(\left( 1 \right)\Leftrightarrow m={{x}^{2}}-2x\).
Xét hàm số \(g\left( x \right)={{x}^{2}}-2x\) có \(g'\left( x \right)=2x-2\). Cho \(g'\left( x \right)=0\Leftrightarrow 2x-2=0\Leftrightarrow x=1\).
Bảng biến thiên của \(g\left( x \right)\)
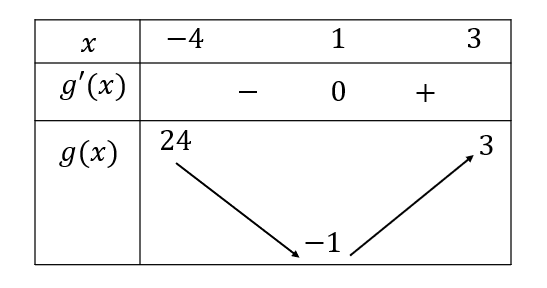
Dựa vào bảng biến thiên ta thấy, phương trình \(\left( 1 \right)\) có 2 nghiệm phân biệt thuộc khoảng \(\left( -4;3 \right)\) khi \(-1<m<3\).
Do \(m\in \mathbb{Z}\Rightarrow m\in \left\{ 0;1;2 \right\}\).
Vậy có 3 giá trị nguyên của tham số \(m\) thỏa yêu cầu đề bài.
Đề thi thử tốt nghiệp THPT môn Toán năm 2023
Trường THPT Gia Định