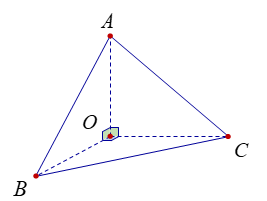
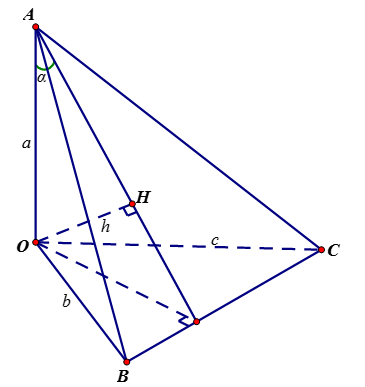
Xét tứ diện (OABC ) có (OA ), (OB ), (OC ) đôi một vuông góc. Gọi \(\alpha, \beta, \gamma \) lần lượt là góc giữa các đường thẳng (OA ), (OB ), (OC ) với mặt phẳng (ABC) (hình vẽ).

Khi đó giá trị nhỏ nhất của biểu thức \( M = \left( {3 + {{\cot }^2}\alpha } \right).\left( {3 + {{\cot }^2}\beta } \right).\left( {3 + {{\cot }^2}\gamma } \right)\)

A. 111

B. 123

C. 124

D. 125

Suy nghĩ và trả lời câu hỏi trước khi xem đáp án

Môn: Toán Lớp 11

Chủ đề: Quan hệ vuông góc trong không gian

Bài: Khoảng cách

Lời giải:

Báo sai

Gọi H là trực tâm tam giác ABC, vì tứ diện OABC có OA, OB, OC đôi một vuông góc nên ta có OH⊥(ABC) và \(\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}\)

Ta có \( \alpha = \widehat {\left( {OA;\left( {ABC} \right)} \right)} = \widehat {OAH},\beta = \widehat {\left( {OB;\left( {ABC} \right)} \right)} = \widehat {OBH},\gamma = \widehat {\left( {OC;\left( {ABC} \right)} \right)} = \widehat {OCH}\)

Nên \( \sin \alpha = \frac{{OH}}{{OA}},\sin \beta = \frac{{OH}}{{OB}},\sin \gamma = \frac{{OH}}{{OC}}\)

Đặt \(a=OA, b=OB, c=OC, h=OH\) thì \( \frac{1}{{{h^2}}} = \frac{1}{{{a^2}}} + \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}}\) và

\(\begin{array}{l} M = \left( {3 + {{\cot }^2}\alpha } \right).\left( {3 + {{\cot }^2}\beta } \right).\left( {3 + {{\cot }^2}\gamma } \right)\\ = \left( {2 + \frac{1}{{{{\sin }^2}\alpha }}} \right).\left( {2 + \frac{1}{{{{\sin }^2}\beta }}} \right).\left( {2 + \frac{1}{{{{\sin }^2}\gamma }}} \right)\\ = \left( {2 + \frac{{{a^2}}}{{{h^2}}}} \right).\left( {2 + \frac{{{b^2}}}{{{h^2}}}} \right).\left( {2 + \frac{{{c^2}}}{{{h^2}}}} \right)\\ = 8 + 4\left( {{a^2} + {b^2} + {c^2}} \right).\frac{1}{{{h^2}}} + 2\left( {{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} \right).\frac{1}{{{h^4}}} + {a^2}{b^2}{c^2}.\frac{1}{{{h^6}}} \end{array}\)

Ta có:

\(\begin{array}{l} \left( {{a^2} + {b^2} + {c^2}} \right).\frac{1}{{{h^2}}} = \left( {{a^2} + {b^2} + {c^2}} \right).\left( {\frac{1}{{{a^2}}} + \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}}} \right) \ge 3\sqrt[3]{{{a^2}.{b^2}.{c^2}}}.3\sqrt[3]{{\frac{1}{{{a^2}}}.\frac{1}{{{b^2}}}.\frac{1}{{{c^2}}}}} = 9\\ \left( {{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} \right).\frac{1}{{{h^4}}} = \left( {{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} \right).{\left( {\frac{1}{{{a^2}}} + \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}}} \right)^2} \ge 3\sqrt[3]{{{a^2}{b^2}.{b^2}{c^2}.{c^2}{a^2}}}.{\left( {3\sqrt[3]{{\left( {\frac{1}{{{a^2}}}.\frac{1}{{{b^2}}}.\frac{1}{{{c^2}}}} \right)}}} \right)^2} = 3\sqrt[3]{{{a^4}{b^4}{c^4}}}.9\sqrt[3]{{\frac{1}{{{a^4}{b^4}{c^4}}}}} = 27{a^2}{b^2}{c^2}.\frac{1}{{{h^6}}}\\ = {a^2}{b^2}{c^2}.{\left( {\frac{1}{{{a^2}}} + \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}}} \right)^3} \ge {a^2}{b^2}{c^2}.{\left( {3\sqrt[3]{{\left( {\frac{1}{{{a^2}}}.\frac{1}{{{b^2}}}.\frac{1}{{{c^2}}}} \right)}}} \right)^3} = 27 \end{array}\)

Do đó:

\( M = 8 + 4\left( {{a^2} + {b^2} + {c^2}} \right).\frac{1}{{{h^2}}} + 2\left( {{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} \right).\frac{1}{{{h^4}}} + {a^2}{b^2}{c^2}.\frac{1}{{{h^6}}} \ge 8 + 4.9 + 2.27 + 27 = 125\)

Dấu đẳng thức xảy ra khi và chỉ khi a=b=ca=b=c, hay OA=OB=OC

Vậy min_M=125